簡介
阿貝正弦條件也稱阿貝正弦律成像原理，是德國物理學家恩斯特·阿貝在1873年發表的光學鏡頭設計的重要成像關係式。
阿貝首先得出阿貝公式：
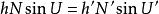阿貝正弦條件其中 N 是 球形曲面物場介質的折射率；
N' 是球形曲面像場介質的折射率；
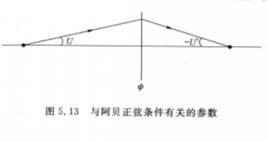
U 是入射光線和光軸的夾角；
U' 是出射光線和光軸的夾角；
h 是物體的高度；
h' 是成像的高度；
當 U 和 U' 角度小的時候，上述阿貝公式簡化為：
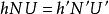阿貝正弦條件這公式早先已被義大利數學家拉格朗日發現，稱為拉格朗日公式。
阿貝公式中的放大率是
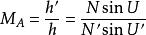阿貝正弦條件拉格朗日公式中放大率是
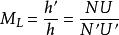阿貝正弦條件在一般情況下 M≠ M，也就是說從鏡頭邊緣折射的大角度光線和從鏡頭中心折射的小角度光線有不同的放大率。
但是恩斯特·阿貝推論：如果鏡頭的球面像差和彗形像差得到完全得修正，這兩個放大率應當相等：
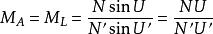阿貝正弦條件由此得出著名的阿貝正弦條件：
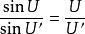阿貝正弦條件阿貝利用阿貝正弦條件這個理論結果配合肖特玻璃廠的新型玻璃為卡爾·蔡司製造出當時最高質量的顯微鏡。
齊明透鏡與齊明點
以兩個折射曲面為邊界的透明體稱為透鏡，通常多以光學玻璃為原材料，磨製成形後將折射面拋光而成。兩個折射面中可以有一個平面，但兩個折射面都是平面者不能稱為透鏡。透鏡由於兩個表面的折射，具有對光束的會聚或發散作用，能在任何要求位置形成物體的像。因此是光學成像系統和照明系統中不可缺少的光學零件。單獨一片透鏡往往不能滿足校正像差的要求；在光學儀器設計過程中經常用幾片透鏡構成組合體，從校正像差的需要出發，確定各透鏡的結構參量，使整個組合體既滿足成像和使用要求，又達到指定的相對孔徑、視場角等光學性能。
與理想成像系統不同的是，實際光學系統只有在近軸區才具有與理想光學系統相同的性質，及只有在孔徑和視場非常小的情況下才能成完善像。實際系統的孔徑和視場都有一定的大小，並且光學系統的功能和使用價值恰恰又與相對孔徑和視場這兩個因素密切相關，因此，實際系統不可能對物體成完善像。
在幾何像差中，如果只討論單色光成像，光學系統會產生5種性質不同的像差，它們分別是球差、慧差、像散、場曲和畸變，統稱為單色像差。在共軸球面系統中，軸上點和軸外點有不同的像差，軸上點因處於軸對稱位置，具有最簡單的像差形式。當軸上物點的物距L確定，並以寬光束孔徑成像時，其像方截距隨孔徑角U（或孔徑高度h）的變化而變化，因此軸上物點發出的具有一定孔徑的同心光束，經光學系統成像後不復為同心光束，
但是，在透鏡的某些特殊點出可以消除像差和彗差。物體在折射面球心時，不產生球差和彗差。物體在不暈點時，不產生球差，彗差，像散，不產生三種像差時稱為“不暈”或“齊明”。如果軸上一對共軛點消球差，且滿足即阿貝正弦條件,則在該軸上物點垂軸方向上的近軸物點也完善成像 (即既無球差，又無彗差)。這樣的共軛點稱為齊明點或不暈點。
