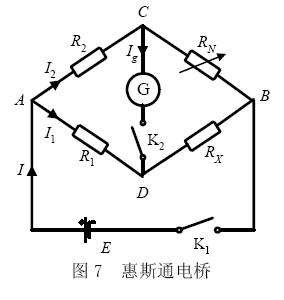
介紹
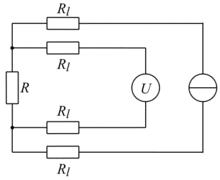開爾文四線檢測原理四線檢測也被稱為開爾文（Kelvin）四線檢測，由威廉·湯姆森·開爾文勳爵（ William Thomson, Lord Kelvin）在1861年發明的開爾文電橋測量低電阻。每兩線連線，可以稱得上是Kelvin連線。
前言
電阻是電路的基本元件之一，電阻值的測量是基本的電學測量。
電阻的分類方法很多，通常按種類劃分稱碳膜電阻、金屬電阻、線繞電阻等：按特性劃分稱固定電阻、可變電阻、特種電阻（光敏電阻，壓敏電阻，熱敏電阻）等；按伏安特性曲線(電壓～電流曲線)的曲直分為線性電阻和非線性電阻（典型非線性電阻有白熾燈泡中的鎢絲、熱敏電阻、光敏電阻、半導體二極體和三極體等）；按阻值大小分為低電阻、中電阻和高電阻。
常用電阻屬於中電阻，其測量方法很多，多數也為大家所熟知。而隨著科學技術的發展，常常需要測量高電阻與超高阻（如一些高阻半導體、新型絕緣材料等），也還需要測量低電阻與超低阻（如金屬材料的電阻、接觸電阻、低溫超導等），對這些特殊電阻的測量，需要選擇合適的電路，消除電路中導線電阻、漏電電阻、溫度等的影響，才能把誤差降到最小，保證測量精度。電橋法是一種用比較法進行測量的方法，它是在平衡條件下將待測電阻與標準電阻進行比較以確定其待測電阻的大小。電橋法具有靈敏度高、測量準確加上方法巧妙，使用方便、對電源穩定性要求不高等特點，已被廣泛地套用於電工技術和非電量電測中。
原理
惠斯通電橋：
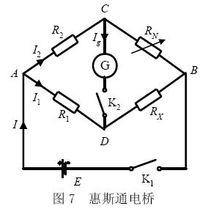開爾文測試惠斯通電橋是惠斯通於1843年提出的電橋電路。它由四個電阻和檢流計組成，RN為精密電阻，RX為待測電阻（電路圖如圖1）。接通電路後，調節R1、R2和RN ，使檢流計中電流為零，電橋達到平衡，此時有RX=RIRN/R2。通過交換測量法(交換RN與RX的位置，不改變RI、R2)得RX=12>nRn'"> .
惠斯通電橋測低電阻的特殊矛盾：
惠斯通電橋（單電橋）測量的電阻，其數值一般在10Ω～1210'> Ω 之間，為中電阻。若用單電橋測低電阻，附加電阻R'與R″（引線電阻和端鈕接觸電阻等）和RX是直接串聯的（如圖2），而R' 和R″ 的大小與被測電阻RX的大小相當、不能被忽略，電阻RN也是小電阻，因此用單電橋測電阻的公式RX=RIRN/R2就不能準確地得出RX的值。
開爾文雙電橋的解決辦法：
開爾文測試開爾文電橋是惠斯通電橋的變形，在測量小阻值電阻時能給出相當高的準確度。其結構如圖3所示，其中R1、R2、R3、R4均為可調電阻，RX為被測低電阻，RN為低值標準電阻。與惠斯通單電橋對比，開爾文電橋做了兩點重要改進：①增加了一個由R2、R4組成的橋臂。
②RN和RX由兩端接法改為四端接法。
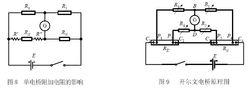
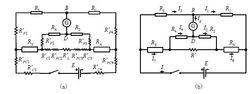
開爾文測試其中P1P2構成被測低電阻RX ，P3P4是標準低電阻RN ，P1P2 、P3P4常被稱為為電壓接點，C1C2、C3C4稱為電流接點。設計思想：將RN和RX的接線電阻和接觸電阻巧妙地轉移到電源內阻和阻值很大的橋臂電阻中（如圖4），又通過R1R4=R2R3和R′≈0的設定，消除了附加電阻的影響，從而保證了測量低電阻時的準確度。具體地，為保證雙電橋的平衡條件，可以有兩種設計方式：
保證R3/R1=R4/R2：a.選定兩組橋臂之比為M=R3/R1=R2/R4，將RN做成可變的標準電阻，調節RN使電橋平衡; b.選定RN為某固定阻值的標準電阻並選定R1=R2為某一值，聯調R3與R4使電橋平衡。
本實驗所用QJ19型單雙電橋採用的是第二種方式。
保證R′≈0：用短粗導線連線Rx與RN。
RX的計算：
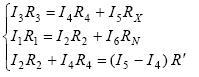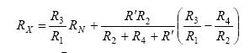開爾文測試
開爾文測試調節R1、R2、R3、R4使電橋平衡。此時，Ig=0，I1= I3，I2 = I4，I5= I6，VB= VD，且有三式聯立求解得
一元線性回歸法：
已知電阻的計算公式為R=ρl/S。
令x≡l,y≡R,並設一元線性回歸方程y=a+bx,其中b=ρ/S。由一元線性回歸法的計算公式求出b，進而求得電阻率ρ=b*S。
實驗中電阻不確定度的計算
計算公式為RX=R1R/R2。測量只進行一次，如果忽略R1、R2在測量過程中數值變動引起的誤差，不確定度只有B類分量，由該電橋儀器誤差引起的不確定度與電橋靈敏度引起的不確定度合成得到。
儀器設備
QJ19型單雙電橋，FMA型電子檢流計，滑線變阻器（48Ω, 2.5A），換向開關，直流穩壓電源（0~3A），四端鈕標準電阻（0.001Ω），待測低電阻（銅桿），電流表（0~3A），數顯示卡尺，中值電阻（阻值約為18kΩ）。
實驗實例
測銅的電阻率
1、按圖5所示連線電路，取電源電壓為15V，調節滑線變阻器是電流表指示為1A；
| 圖5 |
2、由長到短分別測量銅桿不同長度的電阻（每隔5cm測一次，總共至少6次）；3、用數顯示卡尺在銅桿的不同部位測量其直徑多次並記錄。
將QJ19型電橋改為單電橋測量
(中值電阻阻值約18kΩ)
1、將電橋上本應連四端鈕標準電阻的兩端鈕用短路片短接，被測電阻、電源仍接到相應位置（電路圖如圖6所示）；
| 圖6 |
2、接通電源，調測量盤R使電橋平衡，記錄此時的R值及電壓值、電阻值；3、實驗結束後整理儀器。
數據處理和結果討論
測銅的電阻率
原始數據：
| 數據 編號 項目 | 第一組 | 第二組 | 第三組 | 第四組 | 第五組 | 第六組 | |
| 銅桿長度l(cm) | 5 | 10 | 15 | 20 | 25 | 30 | |
| 電阻R（Ω） | 正 | 30.40 | 59.40 | 88.30 | 119.70 | 148.40 | 177.50 |
| 反 | 30.70 | 60.50 | 89.60 | 118.00 | 149.10 | 178.40 | |
| 均 | 30.55 | 59.95 | 88.95 | 118.85 | 148.75 | 177.95 | |
| 電阻R1=R2（Ω） | 100 | ||||||
| 電阻RN（Ω） | 0.001 | ||||||
| 測量次數 | 1 | 2 | 3 | 4 | 5 | 平均 |
| 銅桿直徑d（mm） | 3.95 | 3.96 | 4.00 | 3.98 | 3.96 | 3.97 |
按一元線性回歸法處理數據：
令x≡l,y≡R,並設一元線性回歸方程y=a+bx,其中b=ρ/S。
| i | xi≡li(m) | yi≡Ri(Ω) | xi*xi | yi*yi | xi*yi |
| 1 | 0.05 | 30.55 | 0.0025 | 933.30 | 1.5275 |
| 2 | 0.10 | 59.95 | 0.0100 | 3594.00 | 5.9950 |
| 3 | 0.15 | 88.95 | 0.0225 | 7912.10 | 13.3425 |
| 4 | 0.20 | 118.85 | 0.0400 | 14125.32 | 23.7700 |
| 5 | 0.25 | 148.75 | 0.0625 | 22126.56 | 37.1875 |
| 6 | 0.30 | 177.95 | 0.0900 | 31666.20 | 53.3850 |
| Average | 0.18 | 104.17 | 0.0379 | 13392.92 | 22.5346 |
由一元線性回歸法的計算公式b= , a= -b 求得b=688,r極接近於1，說明R與l高度線性相關。
代入d=3.97mm=3.97*10m，求得電阻率ρ=b*S=bπ /4=0.00851Ω·m。
將QJ19電橋改為單電橋測量電阻
| 測量量 | R1（Ω） | R2（Ω） | R（Ω） | U（V） | A（I） |
| 數據 | 1000 | 10 | 179.76 | 10 | 0.36 |
原始數據：
∴RX=R1R/R2=17.976kΩ
不確定度計算：a.電橋儀器誤差引起的不確定度：
QJ19型單雙電橋的準確度等級為0.05級，比較臂RN的最大值為1011.10Ω,測量時比率C= R1/R2=100,則電橋的有效量程為1011.10x100=101110 Ω,不大於101110的最大10的倍數為100000，故電橋有效量程的基準值R0=100000 Ω.代入得Δ儀=α%(Rx+R0/10)=0.05%x(17976+100000/10) =13.988Ω
u(Δ儀)=Δ儀/√3=8.076。
b.電橋靈敏度誤差引起的不確定度：
當標準電阻改變ΔRN=0.05Ω時，指針偏轉Δn=10格，代入得電橋靈敏度S=ΔnR2/（R1ΔRN）=2，Δ靈=0.2/2=0.1 u（Δ靈）=Δ靈/√3=0.0578.。
合成不確定度: u(Rx)=8.076Ω。
因此測量結果為Rx±u(Rx)=（1.7976±0.0008）Ω。
實驗後思考題
將一量程Ig=50μA，內阻Rg=4.00×10Ω的表頭改裝為一個量程為5A的安培表，並聯的分流電阻是多少？應如何正確連線？ 答：應在安培表兩端並聯一個阻值為4.00×10Ω的分流電阻。 如將QJ19型電橋改為單電橋測銅桿某一長度的電阻，如何進行連線，其結果會怎樣？答：“3”、“4”端鈕用短路片短接，被測電阻接到“5”、“6”端鈕，電源接到“9”、“10”端鈕。如果與儀器“3”、“4”、“7”、“8”連線的四根導線中有一根是斷線，電橋能否調節平衡？若能調節平衡，RX的測量值是否正確？為什麼？答：如果“3”或“8”是斷線，則電路是斷路，電橋不能平衡；如果“4”或“7”是斷線，則RN與Rx之間未連線，相當於RxR4串聯後與R3並聯，R2RN串聯後與R1並聯，電橋能調節平衡，但由於附加電阻的原因Rx的測量值並不準確。
實驗感想與小結
通過本次實驗，我掌握了電橋法測電阻的一般原理，並學會使用了QJ19型單雙電橋、FMA型電子檢流計等以前未使用過的電學實驗儀器，並進一步鞏固了數據處理的一元線性回歸法和不確定度的計算方法，對用Excel等電腦技術解決實際問題更加熟練。
通過“測銅的電阻率”和“將QJ19型電橋改接單電橋測中值電阻”兩個實驗的對比，我對實驗數據的多次測量與否有了較為深入的思考。
1、在“測銅的電阻率”的實驗中，多次測量取平均值減少誤差的思想2次被用到，具體的：
熱電動勢影響的消除。由於線路中電流較大，產生大量焦爾熱。又由於各部分結構不均勻，因而各部分溫度也不均勻，從而會產生附加熱電動勢。考慮到熱電動勢只和IR有關，而與I的方向無關，而電阻上電壓降的正負卻和電流方向有關，故採用改變電流方向的辦法。假定熱電勢與電阻上電壓降原來是相加關係，電流反向後，則成相減關係，從而兩次測得的電阻值一偏大，一偏小，取兩次平均是較好的結果。測銅桿截面圓直徑時，用數顯示卡尺在銅桿的不同部位進行不少於5次的測量，取平均值得銅桿的直徑d。這樣處理減小了因銅桿粗細不均勻而導致的誤差，使計算結果更加精確。2、而在“將QJ19型電橋改接單電橋測中值電阻”的實驗中，由於測量中電路並未改變，並不需要多次測量，因此只測量了一組數據，再通過不確定度的計算對誤差的可能取值範圍進行估計。
