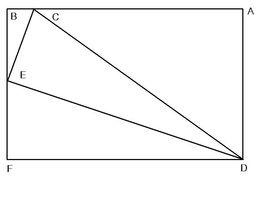
銳角三角比
三角比(trigonometrice ratio)是三角學的基本概念之一,指三角函式定義中的兩線段的數量比。 定義銳角三角函式時,是指含此銳角的直角三角形中任意兩邊的比。定義任意角三角函式時,是指角的終邊上任意一點的縱、橫坐標和原點到這點的距離三個數量中任意兩個的比。
三角比的出現,帶來了角與邊的關係。
銳角三角比又名直角三角比。定義中,都帶有一個“直角三角形”的前提,這是為了方便理解和有一個統一的標準。
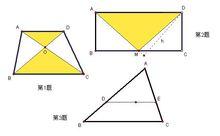 銳角三角比
銳角三角比一個銳角的正切tan(gent)、餘切cot(angent)、正弦sin(e)、餘弦cos(ine),這些三角比的數值,是這個銳角本身自己的“屬性”,和這個角是否在直角三角形中無關。
概念
正切:我們把直角三角形中一個銳角的對邊與鄰邊的比叫做這個銳角的正切(tangent)。
餘切:我們把直角三角形中一個銳角的鄰邊與對邊的比叫做這個銳角的餘切(cotangent)。
正弦:直角三角形中一個銳角的對邊與斜邊的比叫做這個銳角的正弦(sine)。
餘弦:直角三角形中一個銳角的鄰邊與斜邊的比叫做這個銳角的餘弦(cosine)。
正切與餘切的關係:(見右圖)
1.正切:我們把直角三角形中一個銳角的對邊與鄰邊的比叫做這個銳角的正切(tangent)。
2.餘切:我們把直角三角形中一個銳角的鄰邊與對邊的比叫做這個銳角的餘切(cotangent)。
3.正弦:直角三角形中一個銳角的對邊與斜邊的比叫做這個銳角的正弦(sine)。
4.餘弦:直角三角形中一個銳角的鄰邊與斜邊的比叫做這個銳角的餘弦(cosine)。
5.正切與餘切的關係
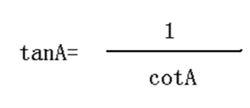 正切與餘切的關係
正切與餘切的關係公式:
tanA=角A的對邊/鄰邊
cotA=角A的鄰邊/對邊
sinA=角A的對邊/斜邊
cosA=角A的鄰邊/斜邊
注意
對於銳角三角函式要注意以下幾點
•要分清一個直角三角形中的對邊和鄰邊。
•三角函式的值是一個比值,這些比值只與銳角的大小有關。當一個銳角的值確定時,它的四個三角函式的值也就確定了。
•任何一個銳角都有四個相應的函式值,不因這個角不在某個直角三角形內而不存在。
•由三角函式的定義可知:0<1;0<1。
•銳角三角函式揭示了三角形中邊與角之間的關係。
•銳角三角比要放在直角三角形中,當書寫時,要先寫在△....中,∠...=90度,然後再開始求值
特殊銳角三角比
| tan | cot | sin | cos | |
| 30° | 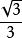 銳角三角比 銳角三角比 | 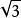 銳角三角比 銳角三角比 |  銳角三角比 銳角三角比 | 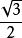 銳角三角比 銳角三角比 |
| 45° | 1 | 1 | 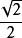 銳角三角比 銳角三角比 | 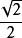 銳角三角比 銳角三角比 |
| 60° | 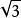 銳角三角比 銳角三角比 | 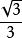 銳角三角比 銳角三角比 | 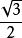 銳角三角比 銳角三角比 |  銳角三角比 銳角三角比 |
| 意義 | 對邊\鄰邊 | 鄰邊\對邊 | 對邊\斜邊 | 鄰邊\斜邊 |
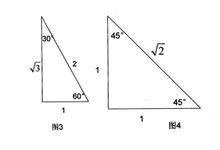 銳角三角比
銳角三角比( √ 為根號)