配極原理及證明
配極原理 配極原理配極原理 如果點P關於二階曲線 的極線p過點Q，則點Q關於二階曲線 的極線q過點P。
利用配極原則可作出二階曲線的切線，同時利用配極原則可以證明某些點的共線問題和某些直線的共點問題 。
配極原理證明 設二階曲線 的方程為
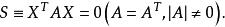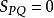配極原理 配極原理 配極原理
配極原理若點P關於 的極線p過點Q，即Q為P關於 的共軛點，它們滿足 。由
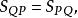配極原理可得
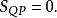配極原理 配極原理 配極原理於是，點P為點Q關於的共軛點，即點Q關於 的極線q過點p 。
相關推論
推論1 兩點連線的極點為此兩點極線的交點；兩直線交點的極線為此兩直線極點的連線(如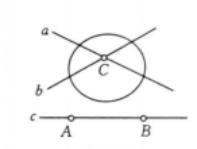圖1)。
圖1推論2 共線點的極線必共點；共點線的極點必共線。
配極原理推論3 設PA、PB為二階曲線的切線，A、B為切點，則直線AB為點P的極線(如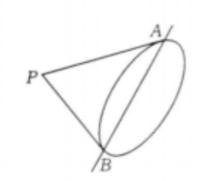圖2) 。
圖2例題解析
配極原理例1 內接於二階曲線的完全四點形的對邊三點形的每個頂點是其對邊的極點。
解：如圖3，PQR為完全四點形ABCD的對邊三點形，於是有
(AB，PE)=-1，(CD，PF)=-1，
配極原理所以點E、F均為點P關於二階曲線的共軛點，從而直線EF即直線QR為點P的極線。
同理，直線PQ為點R的極線，直線RP為點Q的極線 。
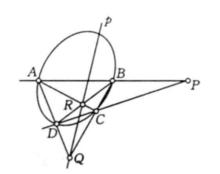圖3例2 已知P不在二階曲線上，求作P的切線 。
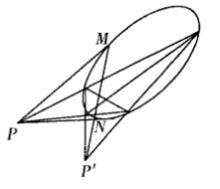圖4解：如圖4，先作出P關於二階曲線的極點P'
PO與二階曲線交於M，N則P'M，P‘’N為所求
因為P過M，則由配極原則，M的極線過P'而M的極線即為P'M。
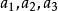配極原理
配極原理
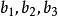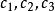配極原理例3 設B'C'，C'A'，A'B'分別是A()，B()，C()關於S=0的極線，求證三點形ABC與A'B'C'透視。
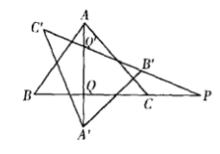圖5如圖5所示，根據配極原理得A',B',C'的極線分別是BC,CA,AB，再設BC與B'C'交於P，AA'與BC,B'C'分別交於Q,Q'，則P的極線是AA'，所以P的極線與A'的極線交於Q，因此Q的極線是PA'。
因B,C,P,Q的極線分別是A'C'，A'B'，A'A，A'P，所以
(BC,PQ)= A'(C'B',AP)
故有 (BC,PQ)=(C'B' ,Q'P)=(B'C',PQ' )，因此BB',CC',QQ'共點，命題得證 。
