傳統PTS算法
部分傳輸序列算法(PTS)最初是由S.H.Muller和J.B.Huber於1997年提出。PTS算法的核心思想是將具有N個符號的輸入序列按照一定的分割方式分割成V個子數據塊，並且保持每個子數據塊仍含有N個符號。然後對V個子數據塊進行相位加權與合併處理，選擇具有最小PAPR的一組符號進行傳輸，達到降低OFDM信號PAPR的目的。
疊代翻轉PTS算法
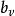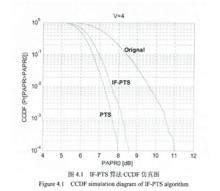
部分傳輸序列IF-PTS算法是由L.J.Cimini和Nelson R. Sollenberger提出，目的就是降低PTS算法的計算複雜度。在IF-PTS算法中相位加權因子，只在{1，-1}中取值，這樣可以儘量降低算法的計算複雜度。IF-PTS算法具體流程:
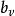部分傳輸序列1、先將N個子載波分割峰V個子序列，令=1 ( v=1,2,..., V)，計算峰均比PAPR；
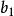部分傳輸序列2、保持=1，並令index=2;
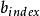部分傳輸序列3、令=一1，計算PAPR';
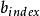部分傳輸序列4、若PAPR< PAPR'，則=--1;否則PAPR= PAPR '，同時令index<V，則返回到第3步;否則，順序執行第5步;
部分傳輸序列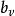 部分傳輸序列5、得到最終的相位加權因子組合。
多層循環PTS算法
ML-PTS算法採用多層循環搜尋方式，可以避免相位因子的搜尋陷入局部最優點，從而增加了搜尋到最佳相位因子組合的機率。因此，與IF-PTS算法相比，ML-PTS算法的PAPR性能得到了顯著的改善。同時ML-PTS算法採用的是循環式的搜尋方法，而不是窮盡式的搜尋方法，因此又避免了算法計算複雜度過高。
