逸度
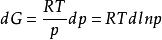 逸度係數
逸度係數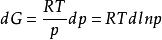 逸度係數
逸度係數由熱力學基本關係式可知,在等溫條件下,dG=Vdp(恆T下);對於1mol純物質,dG=Vdp(恆T下);對於理想氣體,V=RT/p,則 (恆T下),該式形式簡單,但不適用於真實氣體。若將真實氣體狀態方程代入dG=Vdp(恆T下)進行計算,得到的dG將十分複雜。為了保持 的簡單形式,同時又能用於真實氣體,Lewis等提出了用一個新的函式f來代替此式中的p(恆T下):
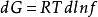 逸度係數
逸度係數在該式中f稱為純物質的逸度,其單位與壓力的單位相同,此式只定義了逸度的相對變化,無法確定其絕對值,為此,規定
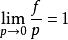 逸度係數
逸度係數作為逸度的補充定義,且該式表明:理想氣體的逸度與壓力相等。
定義
逸度與壓力的比值定義為逸度係數,即
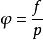 逸度係數
逸度係數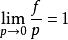 逸度係數
逸度係數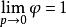 逸度係數
逸度係數根據 可知, 。
真實氣體的逸度係數是溫度、壓力的函式,它可以大於1,也可以小於1。逸度和壓力的單位相同,逸度係數可以理解為壓力的校正係數。
純氣體逸度係數的計算
純氣體逸度(或逸度係數)的計算有如下幾種方法,其中包括用真實氣體狀態方程的解析法、以對應態原理為基礎的普遍化方法以及用pVT數據通過剩餘體積的圖解積分法等,工程上採用的是前兩種方法。
利用狀態方程計算
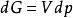 逸度係數
逸度係數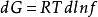 逸度係數
逸度係數由 (恆T下)和 (恆T下)這兩個式子可以得到,在恆T下:
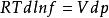 逸度係數
逸度係數在該式等號左右兩邊同時減去RTdlnp,得到:
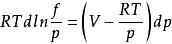 逸度係數
逸度係數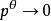 逸度係數
逸度係數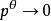 逸度係數
逸度係數在恆T下積分上式,積分下限為 ,上限為p。當壓力 時,氣體可當成理想氣體,積分結果為:
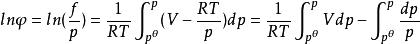 逸度係數
逸度係數上式中右端的第一項改為
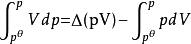 逸度係數
逸度係數接下來的步驟則需要聯繫具體的方程來計算。
利用對應態原理計算
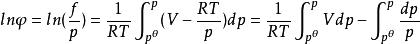 逸度係數
逸度係數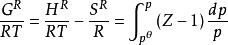 逸度係數
逸度係數由利用狀態方程過程中所得到的方程 結合式 (該式直接表達了真實氣體偏離理想氣體的程度),可得:
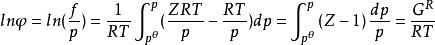 逸度係數
逸度係數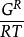 逸度係數
逸度係數上式表明,純物質的逸度或逸度係數直接與量綱為1的剩餘Gibbs函式 相關聯,將其寫成對比態形式,有:
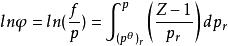 逸度係數
逸度係數 逸度係數
逸度係數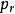 逸度係數
逸度係數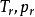 逸度係數
逸度係數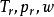 逸度係數
逸度係數上式表明, 是 和Z的函式,而Z的普遍化計算又有以 為參數的參數法和以 為參數的三參數法。
逸度表達式
常用狀態方程的逸度表達式如下:
RK方程
當狀態方程式為RK方程時,對應逸度係數表達式為:
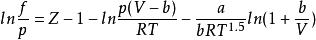 逸度係數
逸度係數SRK方程
當狀態方程式為SRK方程時,對應逸度係數表達式為:
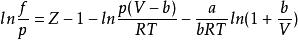 逸度係數
逸度係數PR方程
當狀態方程式為PR方程時,對應逸度係數表達式為:
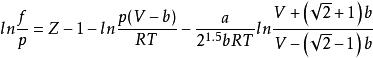 逸度係數
逸度係數Virial方程
當狀態方程式為Virial方程時,對應逸度係數表達式為:
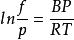 逸度係數
逸度係數MH方程
當狀態方程式為MH方程時,對應逸度係數表達式為:
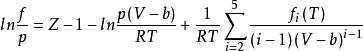 逸度係數
逸度係數
