基本信息
距離是數學中的法則,用在某些空間中測量沿曲線的距離和曲線間的角度,包含曲線所在空間的曲率的信息。這是廣義相對論的中心主題。廣義相對論建立了表示距離度量(因而也是曲率)與物質分布關係的方程。
對於數字圖像中的距離度量,可以表示為:
對於像素p,q和z,其坐標分別為 (x,y),(s,t)和(v,w),如果:
(a) D(p,q)≧0 [D(p,q)=0,若且唯若p=q]
(b) D(p,q)=D(q,p)
(c) D(p,z)≦D(p,q)+D(q,z)
則D是距離函式或者度量。
常見的距離度量有歐氏距離、街區距離、棋盤距離等。
歐氏距離
歐氏距離(Euclid Distance)也稱 歐幾里得度量、歐幾里得距離,是一個通常採用的距離定義,它是在 m維空間中兩個點之間的真實距離。在二維空間中的歐氏距離就是兩點之間的直線段距離。例如,p和q間的歐氏距離定義如下:
De(p,q)=[(x-s)^2+(y-t)^2 ]^1/2
對於距離度量,距點(x,y)的距離小於或等於某一值r的像素是中心在(x,y)且半徑為r的圓平面。
街區距離
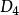 距離度量
距離度量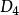 距離度量
距離度量p和q間的距離(4為下標)(又稱城市街區距離)如下定義:
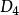 距離度量
距離度量(p,q)=|x-s|+|y-t|
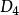 距離度量
距離度量在這種情況下,距(x,y)的距離小於或等於某一值r的像素形成的一個中心在(x,y)的菱形。
不好理解,看例子:距(x,y)的D4距離小於或等於2的像素形成固定距離的下列輪廓:
--- 2
-- 2 1 2
2 1 0 1 2
-- 2 1 2
---- 2
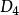 距離度量
距離度量具有=1的像素是(x,y)的4鄰域。
棋盤距離
p和q間的D8(8為下標) 距離(又稱棋盤距離)定義如下式:
D8(p,q)=max(|x-s|,|y-t|)
在這種情況下,距(x,y)的D8距離小於或等於某一值r的像素形成中心在(x,y)的方形。
例如:距點(x,y)(中心點)的D8距離小於或等於2的像素形成下列固定距離的輪廓:
2 2 2 2 2
2 1 1 1 2
2 1 0 1 2
2 1 1 1 2
2 2 2 2 2
具有D8=1的像素是關於(x,y)的8鄰域。
