概念
費曼的路徑積分理論與量子力學曲率解釋在數學意義和物理意義上是完全吻合的。在量子力學曲率解釋中不需要知識波的糾纏，曲率波是真實的物理波，它在時空中的干涉現象直接體現粒子在時空中的真實分布，波與粒子在物理意義上是完全統一的。
費曼路徑積分
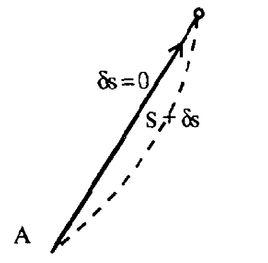
費曼路徑積分根據費曼路徑積分對粒子巨觀軌道的理解，在 取極值 的那條軌道（由一系列的點組成）的鄰域軌道，相位的貢獻均使曲率波幅不是相消，而是相加，總曲率幅大大加強，給出與巨觀粒子對應的明顯的一條可視軌線（如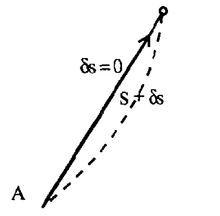圖1）。
圖1在這條軌線上，粒子所經的每一點都具有與軌線鄰域外的點更大的曲率，而軌線鄰域以外的點曲率幅相消得很厲害，空間變得很平坦。
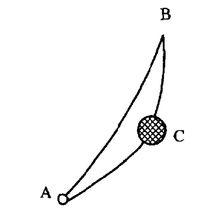圖2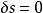 費曼路徑積分 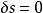費曼路徑積分通過費曼路徑積分的曲率波詮釋，不但能更好地理解微觀世界中的干涉現象，衍射現象也能得到自然的說明。例如，粒子從A到B，如在通路S旁有一障礙物C(如圖2），由於C的遮擋作用，曲率波在B處的傳播必然受到影響，因而到達B點的曲率波的總曲率波幅與C不存在時的情況就有所不同，表現出來的就是衍射現象。與量子現象相反，一個經典的粒子只走 所規定的一條軌道，只要C不橫亘在 的軌道上，就不會對粒子有影響，不會產生衍射現象。
基本原理
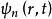費曼路徑積分
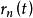費曼路徑積分費曼路徑積分的本質是基於假設波函式 代表粒子經過任意道路 ，從A到B在B點的幾率幅，且傳播子
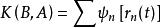費曼路徑積分的平方
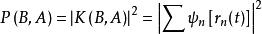費曼路徑積分代表粒子在B點被測到的幾率。
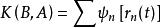費曼路徑積分在 式子中，
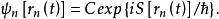費曼路徑積分
費曼路徑積分上式中，為歸一化函式。
其中，
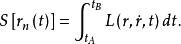費曼路徑積分
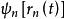費曼路徑積分 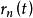費曼路徑積分 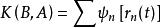費曼路徑積分 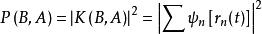費曼路徑積分在量子力學曲率解釋中，波函式代表粒子沿任意路徑從A到B點在B點的曲率波動，式子則代表所有路逕到達B點曲率波的疊加。式子則代表粒子各條路徑在B點形成的疊加態的平方，與總曲率成比例，它表示粒子在B點的可視程度，對應粒子在B點的可測幾率。
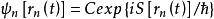費曼路徑積分
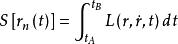費曼路徑積分 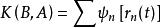費曼路徑積分、兩個式子則表明，粒子從不同途逕到達B點的曲率波振幅雖然相同，但相角卻不同，因而每條路徑傳來的波對B點彎曲的貢獻卻不同。如果B點是變化的，則隨著B點的變化，有些地方是曲率相加，有些地方是曲率相消，故會出現曲率波的干涉現象。實際干涉條紋中，明亮的地方曲率相加，暗的地方曲率相減，條紋的明暗表明曲率大小的變化。實際問題中，各種可能的道路是連續變化的，因而式變為
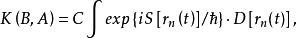費曼路徑積分
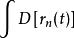費曼路徑積分上式中就是表示對給定初、終點的一切連續變化可能軌道積分。
