負定運算元

設T是希爾伯特空間H上的稠定線性運算元，如果存在實數α，使得對於一切x∈(T)都有(Tx,x)≥α(x,x)（或(Tx,x)≤α(x,x)）成立，就稱T是下半（或上半）有界的。如果α

簡介

半有界運算元

半有界運算元是上半有界運算元和下半有界運算元的統稱。

設T是希爾伯特空間H上的稠定線性運算元，如果存在實數α，使得對於一切x∈(T)都有(Tx,x)≥α(x,x)（或(Tx,x)≤α(x,x)）成立，就稱T是下半（或上半）有界的。

定義

如果α<0，則稱T為負定運算元，並稱α為T的上界。

正定運算元

(positive definite operator)

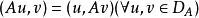負定運算元

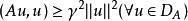負定運算元

正定運算元是相應運算元方程可以化為變分問題的一類重要運算元。設H是實希爾伯特空間，D是H的一個線性稠密子集，A是D→H的線性(不必有界)運算元。如果A是對稱的，即： 且存在正常數γ，使： 則稱A為D上的正定運算元。對D上的正定運算元A，求運算元方程Au=f(f∈H)的解u可以化成求泛函：

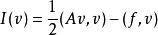負定運算元

取極小值的極值函式u的變分問題。