公式
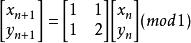 貓映射
貓映射貓映射的原始公式為: ………………………………………………(1)
將其數位化後,得到如下映射
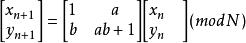 貓映射
貓映射,式中,a、b、N為正整數。………………………………(2)
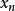 貓映射
貓映射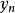 貓映射
貓映射 貓映射
貓映射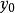 貓映射
貓映射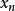 貓映射
貓映射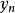 貓映射
貓映射 貓映射
貓映射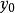 貓映射
貓映射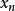 貓映射
貓映射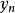 貓映射
貓映射嚴格地說,混沌映射數位化以後獲得的映射不再是混沌的,一個明顯的標誌就是,該映射的軌道全為周期軌道。,而所謂數位化指的是 , (n=0,1,2,…)都為正整數而不是任意實數的情形。故當Nba,,均為正整數時,若初始值 、 也為正整數(對應圖像像素值為整數),則 , (n=0,1,2,…)也都為正整數,貓映射為周期映射。若初始值 、 不為正整數,而是任意實數,則 , (n=0,1,2,…)也都不為正整數而是任意實數,此時貓映射為混沌映射。
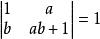 貓映射
貓映射注意貓映射為保面積映射,即滿足 ,當然還有其他的一些形式,只需要滿足保面積的條件即可,故可適當選取其中的一種形式來作為貓映射。
例子
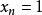 貓映射
貓映射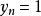 貓映射
貓映射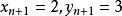 貓映射
貓映射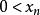 貓映射
貓映射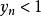 貓映射
貓映射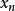 貓映射
貓映射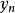 貓映射
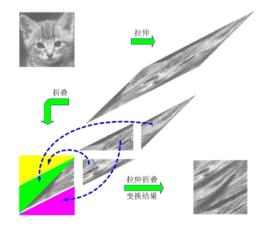
貓映射對於(1)中,是在單位正方形內不斷地進行線性的拉伸,然後通過取模來進行摺疊,從而呈現一種複雜的混沌行為,如圖1所示,顯然,當 , 時, ,將圖中的e點拉伸到圖中的a點,從而將原來左下角的正方形,經過一次貓映射後拉伸成為abcdefa所包圍的圖形,然後再保面積摺疊放回來。在(1)式中,滿足 ,(n=0,1,2,…),即,都是實數。
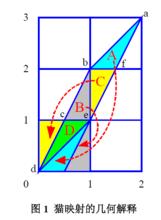 貓映射
貓映射 貓映射
貓映射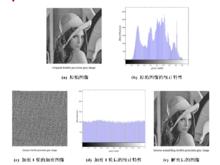 貓映射
貓映射