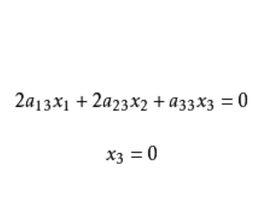變態圓方程
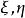 變態圓
變態圓以 表示笛卡爾直角坐標,那么圓的方程可表為:
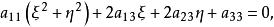 變態圓
變態圓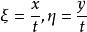 變態圓
變態圓如果用齊次坐標,以 代入上式,就得到
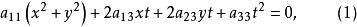 變態圓
變態圓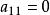 變態圓
變態圓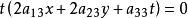 變態圓
變態圓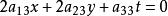 變態圓
變態圓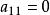 變態圓
變態圓這是在齊次坐標下的圓的方程。當 時,(1)式變為 ,這表示兩條直線 和無窮遠直線t=0,所以當 時,圓分解為兩條直線,其中一條是無窮遠直線, 我們把這兩條直線所組成的二階曲線叫做 變態圓。
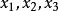 變態圓
變態圓二階曲線的射影定義是兩個射影線束對應直線交點的全體。當這兩個射影線束是透視線束時,對應直線交點的全體稱變態二階曲線。聯接兩線束中心的直線是自對應直線,所以這聯線上任意一點都可以看作是交點。這樣,變態二階曲線是兩直線或者是兩點列,其中一條是兩線束中心聯線, 另一條就是對應直線交點所在直線。變態圓是變態二階曲線,以 為射影齊次坐標,變態圓所在的兩條相交直線為
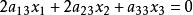 變態圓
變態圓與
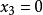 變態圓
變態圓上。
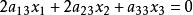 變態圓
變態圓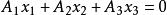 變態圓
變態圓 變態圓
變態圓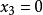 變態圓
變態圓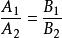 變態圓
變態圓首先,我們看兩線束中心在直線 上的情況。兩線束直線分別以 與 表示。因為對應直線的交點在直線 ,所以必然有 對應直線斜率相等,即 。
定義 在平面的直角坐標系裡,兩虛點(1,i,0)和(1,-i,0)叫做圓點,分別以I,J表示 。
相關定理
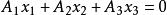 變態圓
變態圓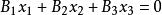 變態圓
變態圓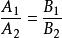 變態圓
變態圓定理1兩線束 與 ,當 為對應直線時,兩線束成透視對應,對應直線交點的全體構成變態圓。
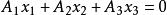 變態圓
變態圓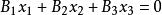 變態圓
變態圓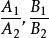 變態圓
變態圓 變態圓
變態圓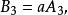 變態圓
變態圓定理2 兩線束 與 (其中 為確定的數且 ),當 (a為非零常數)為對應直線時,兩線束成透視對應,對應直線交點的全體構成變態圓 。
定理3 二階曲線成為圓(常態圓或變態圓)的充要條件是它通過兩個圓點I和J 。
變態圓的射影定義
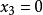 變態圓
變態圓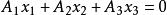 變態圓
變態圓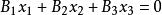 變態圓
變態圓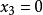 變態圓
變態圓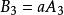 變態圓
變態圓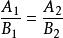 變態圓
變態圓變態圓為兩線束 與 當兩線束中心在直線 上,以 為對應直線交點的全體;當兩線束中心都不在直線上,以 為對應直線交點的全體 。