簡介
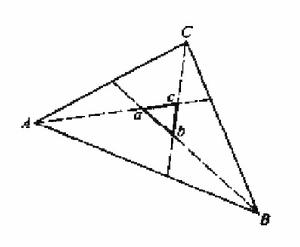
誤差三角形(error triangle)是指用簡化方法求最佳分向點時,當分別由三個不同邊所得的三個分向點位置不能重合而組合的誤差範圍。簡化方法可分別採用支線連線法、力多邊形法、角平分線法或邊線平分法等。誤差範圍內(圖1中abc)任意點均可視為分向點,按星形組合法進行路網規劃的布局方案設計 。
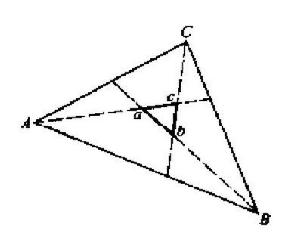 圖1
圖1三標定位
航海上,特別是沿岸航行時,最常用的是兩位置線定位方法,因為它簡單,迅速。但不足之處是:無法直觀地判斷出船位的可靠程度,既使在物標識別、鍘量、標繪等方面存在粗差,也不能反映出來。在這種情況下,如一味地信賴船位,進而進行轉向等一些決策,往往是十分危險的。克服二位置線定位法固有缺陷的方法便是進行三位置線定位。由於同一時刻要獲得三條位置線必須要有三個以上的可觀測物標,所以又叫三標定位。多於三螽以上位置線定位法,其功能與三標定位相同,因過於繁瑣,故極少採用 。
三標定位法的缺點
三標定位法雖能反映出定位過程的可靠性,但也有其缺點,觀測次數增多,定位往往不會交於一點,而是交成一個三角形。這種三角形大小各異、成因有別,所以它們的處理方法也不盡相同。要對三角形進行正確處理,必須首先做到正確鑑別,即找出形成誤差三角形的原因,不外乎有粗差,系統誤差與偶然誤差。粗差乃測者粗心所致,如物標識別錯誤、讀數錯誤等;系統誤差是指某一系統的均值,如羅經差的誤差、計程儀改正率不準等引起的誤差,其特點是大小固定,或能以解析式等形式確切表示 。
偶然誤差
偶然誤差是由一些不確定的偶然因素引起,其特點是單個觀測數據無規律,但許多觀測數據卻呈現一定的規律性,如舍人誤差、繪圖差等。鑒剮三角形成因及其處理方法三角形較小(通常是指在大比例尺海圖上,各邊不超過5毫米)時,認為主要由偶然;誤差引起,處理方法是把船位取在三角形反中線的交點處。三角形較大時,應重新進行測,讀、算、繪等定位過程。如果得到的新三角形仍無多大變化,則認為主要由系統誤差引起。當變化較大(指邊長及方向),剛認為是偶然誤差造成,剛按偶然誤差處理,三角形過大(最大邊長大於1.5海里),則應考慮粗差存在的可能性 。