正文
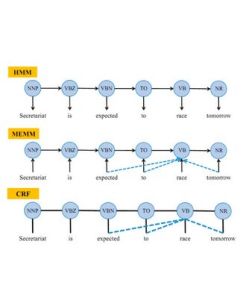
 語言模型
語言模型數理語言學中模擬語言客觀事實的抽象的數學模型。它不完全等同於語言客觀事實,只是語言客觀事實的某種近似物。在語言模型與語言客觀事實之間,可以建立某種對應關係,但是,語言模型不能完全充分地描寫語言客觀事實,它只抽象描寫語言中個別成分(詞、句子等等)的性質及關係(句法、形態等等)。
語言模型與語言客觀事實之間的關係,如同數學上的抽象直線與具體直線之間的關係。
語言模型是一個單純的、統一的、抽象的形式系統,語言客觀事實經過語言模型的描述,比較適合於電子計算機進行自動處理,因而語言模型對於自然語言的信息處理具有重大的意義。
語言模型主要有三種類型:①生成性模型,②分析性模型,③辨識性模型。
生成性模型從一個形式語言系統出發,生成語言的某一集合,如N.喬姆斯基的形式語言理論和轉換語法。
分析性模型從語言的某一集合開始,根據對這個集合中各個元素的性質的分析,闡明這些元素之間的關係,並在此基礎上用演繹的方法建立語言的規則系統,如蘇聯數學家O.C.庫拉金娜和羅馬尼亞數學家S.馬爾庫斯用集合論方法提出的語言模型。
在生成性模型和分析性模型的基礎上,把二者結合起來,便產生了一種很有實用價值的模型,即辨識性模型。辨識性模型可以從語言元素的某一集合及規則系統出發,通過有限步驟的運算,確定這些元素是一堆亂七八糟的詞還是語言中合格的句子。 如Y.巴爾-希列爾用數理邏輯方法提出的句法類型演算模型。