兩個基本原理
加法原理
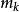 計數原理
計數原理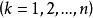 計數原理
計數原理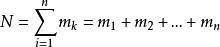 計數原理
計數原理如果一個目標可以在n種不同情況下完成,第k種情況又有 種不同方式來實現 ,那么實現這個目標總共有 種方法。
注意事項:
(1)每種方式都能實現目標,不依賴於其他條件;
(2)每種情況內任兩種方式都不同時存在;
(3)不同情況之間沒有相同方式存在。
乘法原理
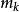 計數原理
計數原理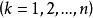 計數原理
計數原理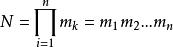 計數原理
計數原理如果實現一個目標必須經過n個步驟,第k步又可以有 種不同方式來實現 ,那么實現這個目標總共有 種方法。
注意事項:
(1)步驟可以分出先後順序,每一步驟對實現目標是必不可少的;
(2)每步的方式具有獨立性,不受其他步驟影響;
(3)每步所取的方式不同,不會得出(整體的)相同方式。
兩個原理異同
加法原理和乘法原理的關鍵點在於區分是分類還是分步。
相同點
加法原理和乘法原理一樣,都是回答有關一件事的不同方法種數的問題。
區別點
加法原理是完成這件事的分類計數方法,每一類都可以獨立完成這件事;乘法原理是完成這件事的分步計數方法,每個步驟都不能獨立完成這件事。
套用這兩個原理解題,首先應該分清要完成的事情是什麼,然後需要區分是分類完成還是分步完成,“類”間相互獨立,“步”間相互聯繫。
典例
例1
求以下要求的計數。
A:大於0小於10的偶數;
B:大於0小於10的奇數;
C:大於0小於10的整數;
D:大於0小於10的質數。
E:大於0小於10的質數或偶數。
解:
(1)A={2,4,6,8},|A|=4;
(2)B={1,3,5,7,9},|B|=5;
(3)C=A∪B,|C|=|A|+|B|=9;
(4)D={1,2,3,5,7},|D|=5;
(5)E=A∪D,但質數與偶數並不互斥,有一個公共元素2,故有|E|=|A|+|D|-1=4+5-1=8。
例2
從A地到B地共有3種方法,從B地到C地共有兩種方法,問從A地到C地共有多少種方法。
解:要從A地到C地,需要先從A到B,再從B到C,且A到B的3種方法和B到C的2種方法互不干擾,故總共有3×2=6種方法。

