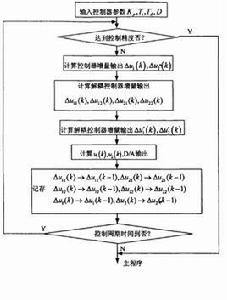
解耦思想的提出
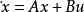 解耦算法
解耦算法在多變數系統中,由於被控對象各個通道之間相互鉸鏈,一個輸入信號的變化會引起多個輸出量的變化,每個輸出也不止受一個輸入的影響,系統的這種相互關聯稱之為藕合,在存在著耦合的系統中,即使精心選擇輸出與控制輸入之間的配對關係,也難免存在相關現象,所以使輸出獨立地跟蹤各自的設定值有一定困難。這時,再設計相應的控制器來跟蹤系統的輸入就比較容易了。解耦控制的思想最早是由Gilbert E.G.完成的。當時稱為Morgan問題。解耦問題是多輸入多輸出(MIMO)線性定常系統綜合理論的一個重要組成部分。其目的是尋找合適的控制規律使閉環控制系統實現一個輸出分量僅僅受一個輸入分量控制,而且不同的輸出分量受不同的輸入分量控制,從而可以運用經典的控制系統綜合方法進行系統校正,以使系統的動靜態性能及各項指標滿足工程需要 。
解耦方法分類
根據解耦的程度,解耦可分為全解耦和近似解耦;根據解耦的時間特性,解耦又可分為靜態解耦和動態解耦。對於確定的線性多變數系統,可採用對角矩陣法,相對增益分析法,反Nyquist曲線法,特徵曲線分析法,狀態變數法,序列回差法等傳統的解耦方法進行控制。但是複雜工業過程中的系統存在著多變數、強耦合、非線性、動態特性變化大、生產工況變化頻繁等情形,這時傳統的解耦方法就不適用了,因而產生了新的多變數解耦控制方法。將自適應控制、模糊控制與解耦控制相結合併用於多變數系統中,就形成了多種解耦控制方法 。
傳統解耦方法
傳統解耦方法以現代頻域法為代表,也包括時域方法,主要適用於線性定常多輸入多輸出系統。
自適應解耦方法
自適應控制的思想與解耦技術相結合併用於多變數系統中,就形成了自適應解耦方法。自適應解耦的目標是使系統的閉環傳遞函式成為對角陣,通常把耦合信號作為干擾處理。自適應解耦實質上採用了最優控制的方法,建立目標函式並對參數尋優是該方法的核心,這是與傳統解耦方法的本質區別,是解耦理論的重大突破,同時也是智慧型解耦理論的基礎。自適應解耦可適用於時變對象。
智慧型解耦方法
智慧型解耦方法以神經元網路解耦方法為代表。由於神經網路可實現多輸入到多輸出的映射,以任意精度逼近任意函式,並具有自學習功能,因此適用於時變、非線性、特性未知的對象 。
解耦算法
選擇適當的控制規律將一個多變數系統化為多個獨立的單變數系統的控制問題。在解耦控制問題中,基本目標是設計一個控制裝置,使構成的多變數控制系統的每個輸出變數僅由一個輸入變數完全控制,且不同的輸出由不同的輸入控制。
解耦原理
對於輸出和輸入變數個數相同的系統,如果引入適當的控制規律,使控制系統的傳遞函式矩陣為非奇異對角矩陣,就稱系統實現了完全解耦。使多變數系統實現完全解耦的控制器,既可採用狀態反饋結合輸入變換的形式,也可採用輸出反饋結合補償裝置的形式。
已證明,系統可用狀態反饋和輸入變換,即通過引入控制規律 u=- Kx+ Lv,實現完全解耦的充分必要條件是矩陣E為非奇異。這裡, u為輸入向量, x為狀態向量, v為參考輸入向量, K為狀態反饋矩陣, L為輸入變換矩陣。對於滿足可解耦性條件的多變數系統,通過將它的係數矩陣 A , B , C化成為解耦規範形,便可容易地求得所要求的狀態反饋矩陣 K和輸入變換矩陣 L。完全解耦控制方式的主要缺點是,它對系統參數的變動很敏感,系統參數的不準確或者在運行中的某種漂移都會破壞完全解耦。
算法流程圖
解耦控制算法流程圖如圖所示 。
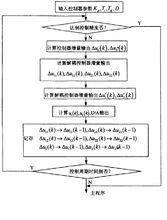 解耦算法
解耦算法