基本介紹
 角微商
角微商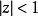 角微商
角微商 角微商
角微商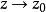 角微商
角微商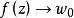 角微商
角微商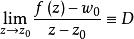 角微商
角微商 角微商
角微商 角微商
角微商設在內全純,如果沿以單位圓周上的點為終點的Stolz道路時,一致地有,且極限存在,則稱D為在處的 角微商(angular derivative)。
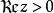 角微商
角微商 角微商
角微商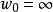 角微商
角微商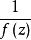 角微商
角微商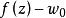 角微商
角微商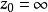 角微商
角微商 角微商
角微商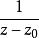 角微商
角微商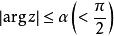 角微商
角微商 角微商
角微商在域是半平面的情形,對虛軸上的點也可同樣地定義角微商。但是,當時,在上式中要用代替,而當時,要用代替,在後面這種情形,Stolz道路理解為包含於角域內的趨於的道路。角微商的研究由G.Julia(1920),J.Wolff(1926)開始,而由Carathéodory(1929),E.Landau-G,Valiron(1929)推進 。
相關結論
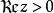 角微商
角微商 角微商
角微商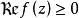 角微商
角微商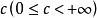 角微商
角微商 角微商
角微商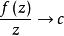 角微商
角微商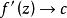 角微商
角微商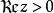 角微商
角微商 角微商
角微商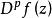 角微商
角微商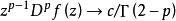 角微商
角微商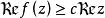 角微商
角微商關於角微商的基本定理可敘述如下:若在內全純的函式滿足,則存在常數,使當z沿Stolz道路趨於時,一致地有和;且對任意的正整數p,對於的p階導數,還一致地成立。此外,在內,處處成立。單位圓的情形也有類似的定理。
 角微商
角微商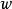 角微商
角微商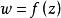 角微商
角微商 角微商
角微商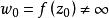 角微商
角微商對於保角映射理論,研究把平面上的單位圓(或半平面)D映射到平面的單連通域B上的函式,在D的邊界上的一點處具有非零的有限角微商的條件,也即在邊界上兼有保角性和線素比不變性的條件,是重要的。Carathéodory指出,使這一點成立的一個充分條件是:存在分別在B的外部和內部的兩個圓周,它們在B的邊界點處互相外切或內切。接著,L.Ahlfors利用關於帶形域的畸變定理,導出了角微商存在的充分必要條件,Wolff在保角映射的疊代的研究中套用了角微商 。