背景
1973年,Li和Yorke使用混沌(chaos)一詞來研究混沌的特性,從而拉開了混沌研究的序幕。30年來,混沌已經成為一項熱門話題。非線性動力學已經成為內容極為豐富,套用範圍極其廣泛的研究領域。混沌現象是發生在確定性系統中的一種不確定行為,具體表現在混沌系統具有分維吸引子和對初值敏感性,由於非線性動力學系統的運動狀態失穩而出現分岔以至於混沌狀態是非常普遍的現象。
文獻 提出了混沌可加性的概念,從理論上證明兩個或兩個以上混沌序列的可加性,計算機模擬表明新的混沌系統動力學行為具有分維吸引子和對初值敏感性。
動力學模型
 複合混沌系統
複合混沌系統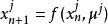 複合混沌系統
複合混沌系統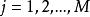 複合混沌系統
複合混沌系統若有 個混沌系統 ,其動力學差分方程為 ,
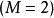 複合混沌系統
複合混沌系統首先考慮兩個混沌系統 ,則上式可以改寫為:
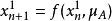 複合混沌系統
複合混沌系統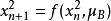 複合混沌系統
複合混沌系統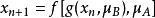 複合混沌系統
複合混沌系統複合構成的新系統的基本形式為
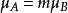 複合混沌系統
複合混沌系統 複合混沌系統
複合混沌系統設 ,如果 ,且兩個混沌系統的系統參數相等,則完全相同結構的複合形式混沌系統為
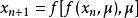 複合混沌系統
複合混沌系統 複合混沌系統
複合混沌系統如果 ,且兩個混沌系統為不同結構,則複合結構的新混沌系統為:
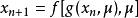 複合混沌系統
複合混沌系統 複合混沌系統
複合混沌系統二維混沌系統的兩個變數方向上分別有兩種複合形式,在 變數方向上
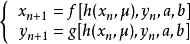 複合混沌系統
複合混沌系統 複合混沌系統
複合混沌系統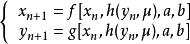 複合混沌系統
複合混沌系統在 變數方向上,
以上給出了兩種一維混沌系統及其兩種一維和二維混沌系統的複合構成方式。由於混沌系統的複合形式很多,尤其是高維混沌系統和不同結構混沌系統的多重複合更為複雜。
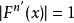 複合混沌系統
複合混沌系統各種複合系統的分岔序列和簡單混沌系統的分岔序列有相似的規律,可以使用不動點的確定方法和 得出具體的分岔序列。
套用
以複合混沌系統在加密系統方面的套用為例。
近年來,利用混沌來研製新的加密系統引起了人們的廣泛重視。由於混沌系統對初值條件和系統參數非常敏感,其生成的混沌序列具有寬頻譜、類噪聲、可精確再生和難以長期預測等特點,使混沌在加密和保密通信中具有潛在的套用價值。因此,藉助混沌系統可望設計出容易控制和具有高安全性的加密系統。
 複合混沌系統
複合混沌系統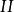 複合混沌系統
複合混沌系統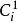 複合混沌系統
複合混沌系統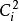 複合混沌系統
複合混沌系統複合混沌加密系統如圖1所示。圖1中混沌系統 由Chen系統構成,混沌系統由Logistic混沌映射構成,兩個系統分別在第i時刻輸出混沌序列和。
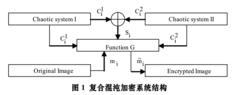 複合混沌系統
複合混沌系統序列產生規則如下:
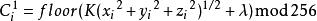 複合混沌系統
複合混沌系統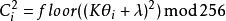 複合混沌系統
複合混沌系統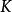 複合混沌系統
複合混沌系統 複合混沌系統
複合混沌系統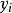 複合混沌系統
複合混沌系統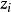 複合混沌系統
複合混沌系統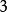 複合混沌系統
複合混沌系統 複合混沌系統
複合混沌系統 複合混沌系統
複合混沌系統 複合混沌系統
複合混沌系統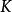 複合混沌系統
複合混沌系統 複合混沌系統
複合混沌系統其中,,和是Chen系統的個狀態變數在第時刻的值,為Logistic系統在第時刻的值,而和為控制參數。混沌系統對初值條件很敏感,但是當初值條件有微小差異時,這種敏感性是需要系統經歷一段演化時間才會充分體現出來。因此,為了適應圖像這種大數據量對加密速度的需求,用一個因子去放大這種敏感性。
