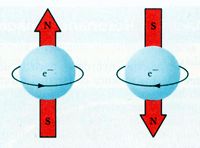
定義及發展
自鏇量子數是描述電子自鏇運動的量子數。是電子運動狀態的第四個量子數。1921年,德國施特恩(Otto Stern,1888—1969)和格拉赫(Walter Gerlach,1889—1979)在實驗中將鹼金屬原子束經過一不均勻磁場射到螢幕上時,發現射線束分裂成兩束,並向不同方向偏轉。這暗示人們,電子除了有軌道運動外,還有自鏇運動,是自鏇磁矩順著或逆著磁場方向取向的結果。於是1925年荷蘭物理學家烏侖貝克(George Uhlenbeck,1900—1988)和哥希密特(Goudsmit,1902—1978)提出電子有不依賴於軌道運動的、固有磁矩(即自鏇磁矩)的假設。自鏇量子數s≡1/2,它是表征自鏇角動量的量子數,相應於軌道角動量量子數。自鏇磁量子數ms才是描述自鏇方向的量子數。ms= 1/2,表示電子順著磁場方向取向,用↑表示,說成逆時針自鏇;ms=-1/2表示逆著磁場方向取向,用↓表示,說成順時針自鏇。當兩個電子處於相同自鏇狀態時叫做自鏇平行,用符號↑↑或↓↓表示。當兩個電子處於不同自鏇狀態時,叫做自鏇反平行,用符號↑↓或↓↑表示。
直接從Schrödinger方程得不到第四個量子數——自鏇量子數ms,它是根據後來的理論和實驗要求引入的。精密觀察強磁場存在下的原子光譜,發現大多數譜線其實由靠得很近的兩條譜線組成。這是因為電子在核外運動,還可以取數值相同,方向相反的兩種運動狀態,通常用↑和↓表示。
自鏇的分類
基本粒子的自鏇
對於像光子、電子、各種夸克這樣的基本粒子,理論和實驗研究都已經發現它們所具有的自鏇無法解釋為它們所包含的更小單元圍繞質心的自轉(參見經典電子半徑)。由於這些不可再分的基本粒子可以認為是真正的點粒子,因此自鏇與質量、電量一樣,是基本粒子的內稟性質。
在量子力學中,任何體系的角動量都是量子化的,其取值只能為:
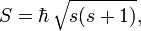 S
S其中 h 是約化普朗克常數,而自鏇量子數是整數或者半整數(0, 1/2, 1, 3/2, 2,……),自鏇量子數可以取半整數的值,這是自鏇量子數與軌道量子數的主要區別,後者的量子數取值只能為整數。自鏇量子數的取值只依賴於粒子的種類,無法用現有的手段去改變其取值(不要與自鏇的方向混淆,見下文)。
例如,所有電子具有s = 1/2,自鏇為1/2的基本粒子還包括正電子、中微子和夸克,光子是自鏇為1的粒子,理論假設的引力子是自鏇為2的粒子,理論假設的希格斯玻色子在基本粒子中比較特殊,它的自鏇為0。
亞原子粒子的自鏇
對於像質子、中子及原子核這樣的亞原子粒子,自鏇通常是指總的角動量,即亞原子粒子的自鏇角動量和軌道角動量的總和。亞原子粒子的自鏇與其它角動量都遵循同樣的量子化條件。
通常認為亞原子粒子與基本粒子一樣具有確定的自鏇,例如,質子是自鏇為1/2的粒子,可以理解為這是該亞原子粒子能量低的自鏇態,該自鏇態由亞原子粒子內部自鏇角動量和軌道角動量的結構決定。
利用第一性原理推導出亞原子粒子的自鏇是比較困難的,例如,儘管我們知道質子是自鏇為1/2的粒子,但是原子核自鏇結構的問題仍然是一個活躍的研究領域。
原子和分子的自鏇
原子和分子的自鏇是原子或分子中未成對電子自鏇之和,未成對電子的自鏇導致原子和分子具有順磁性。
自鏇與統計
粒子的自鏇對於其在統計力學中的性質具有深刻的影響,具有半整數自鏇的粒子遵循費米-狄拉克統計,稱為費米子,它們必須占據反對稱的量子態(參閱可區分粒子),這種性質要求費米子不能占據相同的量子態,這被稱為泡利不相容原理。另一方面,具有整數自鏇的粒子遵循玻色-愛因斯坦統計,稱為玻色子,這些粒子可以占據對稱的量子態,因此可以占據相同的量子態。對此的證明稱為自鏇統計理論,依據的是量子力學以及狹義相對論。事實上,自鏇與統計的聯繫是狹義相對論的一個重要結論。
發現
自鏇的發現,首先出現在鹼金屬元素的發射光譜課題中。於1924年,沃爾夫岡·泡利首先引入他稱為是「雙值量子自由度」(two-valued quantum degree of freedom),與最外殼層的電子有關。這使他可以形式化地表述泡利不相容原理,即沒有兩個電子可以在同一時間共享相同的量子態。
泡利的「自由度」的物理解釋最初是未知的。Ralph Kronig,Landé的一位助手,於1925年初提出它是由電子的自轉產生的。當泡利聽到這個想法時,他予以嚴厲的批駁,他指出為了產生足夠的角動量,電子的假想表面必須以超過光速運動。這將違反相對論。很大程度上由於泡利的批評,Kronig決定不發表他的想法。
當年秋天,兩個年輕的荷蘭物理學家產生了同樣的想法,George Uhlenbeck和Samuel Goudsmit。在保羅·埃倫費斯特的建議下,他們以一個小篇幅發表了他們的結果。它得到了正面的反應,特別是在Llewellyn Thomas消除了實驗結果與 Uhlenbeck 和 Goudsmit 的(以及 Kronig 未發表的)計算之間的兩個矛盾的係數之後。這個矛盾是由於電子指向的切向結構必須納入計算,附加到它的位置上;以數學語言來說,需要一個纖維叢描述。切向叢效應是相加性的和相對論性的(比如在c趨近於無限時它消失了);在沒有考慮切向空間朝向時其值只有一半,而且符號相反。因此這個複合效應與後來的相差係數2(Thomas precession)。
儘管他最初反對這個想法,泡利還是在1927年形式化了自鏇理論,運用了埃爾文·薛丁格和沃納·海森堡發現的現代量子力學理論。他開拓性地使用泡利矩陣作為一個自鏇運算元的群表述,並且引入了一個二元鏇量波函式。
泡利的自鏇理論是非相對論性的。然而,在1928年,保羅·狄拉克發表了狄拉克方程式,描述了相對論性的電子。在狄拉克方程式中,一個四元鏇量所謂的「狄拉克鏇量」被用於電子波函式。在1940年,泡利證明了「自鏇統計定理」,它表述了費米子具有半整數自鏇,玻色子具有整數自鏇。
自鏇電子學
瑞典皇家科學院表示,2007年諾貝爾物理學獎獎勵的是從電腦硬碟讀取數據的技術根源。法國科學家費爾和德國科學家格林貝格爾1988年發現的巨磁電阻效應,大大提高了器件性能,使我們的計算機硬碟體積越來越小,而容量越來越大。
然而,這項發現的偉大之處還不僅如此。《科學時報》記者就此採訪了該領域4位學者。其中中國科學院物理研究所研究員朱濤表示:“費爾和格林貝格爾種下了一粒種子,隨著20世紀90年代套用的突破,這粒種子長成了一棵小苗——自鏇電子學,這是一個成長很快、前景廣闊的磁學分支。”
套用
自鏇的直接的套用包括:核磁共振譜、電子順磁共振譜、質子密度的磁共振成像,以及巨磁電阻硬碟磁頭。自鏇可能的套用有自鏇場效應電晶體等。以電子自鏇為研究對象,發展創新磁性材料和器件的學科分支稱為自鏇電子學。