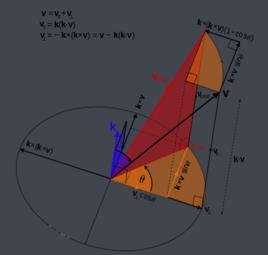
發現歷程和定義
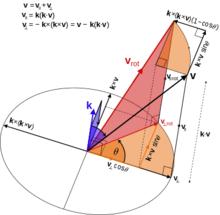 羅德里格旋轉公式
羅德里格旋轉公式在向量旋轉公式發現以前,瑞士數學家列昂哈德·歐拉(Leonhard Euler(1707-1783))為了證明四平方和定理,發現了四平方和恆等式。然而這個恆等式的構造過程非常繁瑣。直到後來,四元數被引入,使得這個恆等式的推導大大簡化。
四元數可以很方便地表示旋轉變換。但在很多場合中,使用矩陣形式和向量形式表達旋轉更有利於推導。向量旋轉公式 最早由法國數學家班傑明·奧倫德·羅德里格 (Benjamin Olinde Rodrigues(1795–1851))導出,後來被套用在很多領域。
設 v是一個三維空間向量, k是旋轉軸的單位向量,則 v在右手螺旋定則意義下繞旋轉軸 k旋轉角度 θ得到的向量可以由三個不共面的向量 v, k和 k× v構成的標架表示:
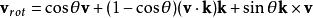 羅德里格旋轉公式
羅德里格旋轉公式推導
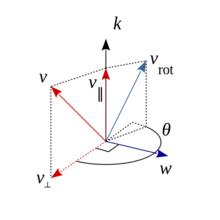 羅德里格旋轉公式
羅德里格旋轉公式 羅德里格旋轉公式
羅德里格旋轉公式 羅德里格旋轉公式
羅德里格旋轉公式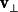 羅德里格旋轉公式
羅德里格旋轉公式 羅德里格旋轉公式
羅德里格旋轉公式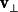 羅德里格旋轉公式
羅德里格旋轉公式如果被旋轉向量 v與旋轉軸 k(k為單位向量)相互垂直,那旋轉變換不難表示。而對於與旋轉軸 k呈任意角度的向量 v,可以通過正交分解,把被旋轉向量轉化為與旋轉軸平行的分量 和與旋轉軸垂直的分量 ,其中與旋轉軸平行的分量 在旋轉中是不變的,而與旋轉軸垂直的分量 則恰好旋轉了角度 θ,把與旋轉軸平行的分量與旋轉以後的與旋轉軸垂直的分量加在一起,即可得到旋轉以後的向量。
第一步是如何對向量 v做正交分解:
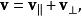 羅德里格旋轉公式
羅德里格旋轉公式 羅德里格旋轉公式
羅德里格旋轉公式利用向量投影公式,可以得到 的表達式:
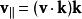 羅德里格旋轉公式
羅德里格旋轉公式通過做減法,得到
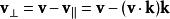 羅德里格旋轉公式
羅德里格旋轉公式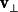 羅德里格旋轉公式
羅德里格旋轉公式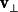 羅德里格旋轉公式
羅德里格旋轉公式利用外積可以計算與 和 k都垂直,且長度等於 的向量 w:
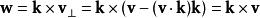 羅德里格旋轉公式
羅德里格旋轉公式旋轉以後的向量可以表示為:
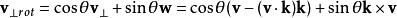 羅德里格旋轉公式
羅德里格旋轉公式 羅德里格旋轉公式
羅德里格旋轉公式與 相加即可得到旋轉以後的向量表達式:
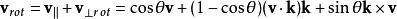 羅德里格旋轉公式
羅德里格旋轉公式矩陣形式
在計算機圖形學中,羅德里格向量旋轉公式通常被用來填寫旋轉矩陣。如果把 k和 v分別寫為列向量:
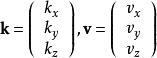 羅德里格旋轉公式
羅德里格旋轉公式則旋轉以後的向量可以表示為:
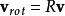 羅德里格旋轉公式
羅德里格旋轉公式其中
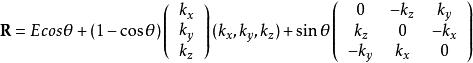 羅德里格旋轉公式
羅德里格旋轉公式其中E是3階單位矩陣。需要注意的是,公式中的第二項不是點積,而是張量積,得到的是一個3行3列的矩陣。
理論力學中的套用
在理論力學中,旋轉非慣性系中的物體都要受到慣性離心力和科里奧利力的作用。可以用羅德里格向量旋轉公式推導這些力的大小。
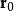 羅德里格旋轉公式
羅德里格旋轉公式設在以角速度ω,繞單位向量 k旋轉的慣性系中,物體在 處以速度 v運動,則物體在該局部坐標系下的運動方程為:
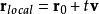 羅德里格旋轉公式
羅德里格旋轉公式而在靜止參考系統中,物體的運動方程為:
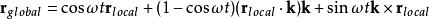 羅德里格旋轉公式
羅德里格旋轉公式上式對 t求導,可得到物體的絕對速度
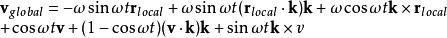 羅德里格旋轉公式
羅德里格旋轉公式再對 t求導,得到物體的加速度
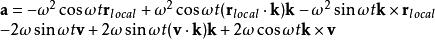 羅德里格旋轉公式
羅德里格旋轉公式在t=0時刻,有
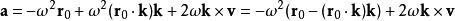 羅德里格旋轉公式
羅德里格旋轉公式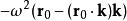 羅德里格旋轉公式
羅德里格旋轉公式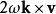 羅德里格旋轉公式
羅德里格旋轉公式即為物體的加速度。其中為向心加速度,為科氏加速度。根據牛頓第二定律,即可得出慣性離心力和科里奧利力的計算公式 。