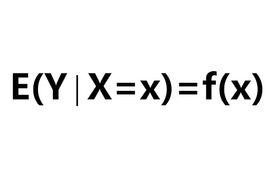定義
總體回歸函式
總體回歸函式在給定解釋變數 條件下被解釋變數 的期望軌跡稱為總體回歸線（population regression line），或更一般地稱為總體回歸曲線（population regression curve）。相應的函式
總體回歸函式 總體回歸函式E(Y/ )=f( )
總體回歸函式 總體回歸函式稱為(雙變數)總體回歸函式(population regression function，PRP)。將居民消費支出看成是其可支配收入的線性函式時，式子E(Y/ )=f( )可進一步寫成
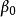總體回歸函式
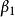總體回歸函式
總體回歸函式 總體回歸函式E(Y∣ )= +
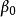總體回歸函式 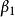總體回歸函式其中， 、 是未知參數．稱為回歸係數(regression coefficients)。上式也稱為線性總體回歸函式。
方程形式與套用
總體回歸函式 總體回歸函式所採取的函式形式，是由所考察總體固有的特徵來決定的。由於實踐中總體往往無法全部考察到，因此總體回歸函式形式的選擇就是一個經驗方面的問題，這時經濟學等相關學科的理論就顯得很重要。例如，生產函式常以Cobb-Douglas冪函式的形式出現，U形邊際成本函式以二次多項式的形式出現等。將居民消費支出看成是其可支配收入的線性函式時，式子E(Y/ )=f( )可進一步寫成
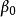總體回歸函式 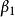總體回歸函式 總體回歸函式 總體回歸函式E(Y∣ )= +
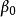總體回歸函式 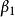總體回歸函式其中， 、 是未知參數．稱為回歸係數(regression coefficients)。上式也稱為線性總體回歸函式
線性函式形式最為簡單，其中參數的估計與檢驗也相對容易，而且多數非線性函式可轉換為線性形式，因此，為了研究的方便．計量經濟學中總體回歸函式常設定成線性形式。需注意的是，經典計量經濟方法中所涉及的線性函式，指回歸係數是線性的，即回歸係數只以它的一次方出現，對解釋變數則可以不是線性的 。
(1)在總體同歸函式中．當f(x)為線性函式時．稱為線性回歸(Linear regression)；
(2)當f(x)為非線性函式時,稱為非線性回歸(Nonlinear regression)；
(3)當f(x)中的自變數只有一個時,稱為一元回歸；
(4)當f(x)中的自變數多於一個時,稱為多元回歸．
舉例：
若
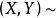總體回歸函式
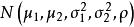總體回歸函式則有條件分布
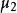總體回歸函式
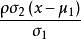總體回歸函式
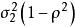總體回歸函式Y∣X=x~N(+,).
從而有總體回歸函式
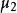總體回歸函式 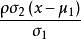總體回歸函式E(Y∣X=x)=+.
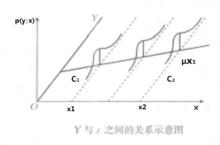
如圖所示，線性函式形式最為簡單．其中參數的估計與檢驗也相對容易．而且很多非線性函式可轉換為線性形式，因此．為了研究方便，總體回歸函式常設定成線性形式．
總體回歸函式