微分方程的線性化
嚴格的講,實際物理原件和系統都是非線性的。
疊加原理不適應於非線性系統,這給求解非線性系統帶來了不便,因此需要對所研究的系統做線性化處理。
非線性系統的線性化
非線性系統進行線性化的條件:
非線性函式是連續函式;系統在預定工作點附近小偏差運行,即變數的變化範圍很小。
單變數系統的線性化
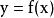 線性化
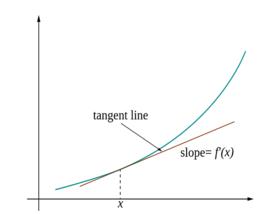
線性化如圖1所示為連續變化的非線性函式為:
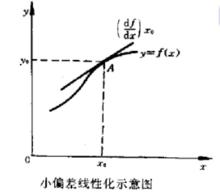 圖1
圖1線性化方法:
 線性化
線性化把非線性函式在工作點 附近展開成泰勒級數,略去高次項,使得一個以增量為變數的線性函式:
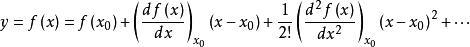 線性化
線性化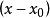 線性化
線性化當增量 很小時,略去其高次冪項,則
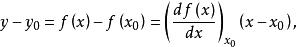 線性化
線性化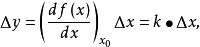 線性化
線性化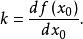 線性化
線性化 線性化
線性化k是比例係數,它是函式 在工作點A點的切線斜率。
將線性增量方程代入系統微分方程,便可得系統線性化方程。
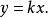 線性化
線性化多變數函式的線性化
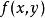 線性化
線性化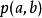 線性化
線性化在函式 的一個點 處的線性化函式是:
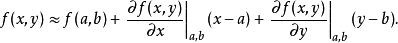 線性化
線性化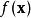 線性化
線性化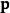 線性化
線性化多變數函式的一般方程 在一個點 處的線性化方程是:
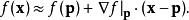 線性化
線性化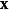 線性化
線性化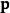 線性化
線性化其中 是變數的向量, 是線性化的工作點 。
線性化總結
1)線性化是相隨某已工作點,工作點不同,線性化方程的係數也不同;
2)偏差越小,線性化精度越高;
3)線性化適用於連續變化的單值函式;
4)式中變數是增量,不是絕對值,公式稱為增量方程式;
5)額定工作點若是坐標原點,增量可以寫成絕對量;
6)當增量並不是很小時,在進行線性化時,為了驗證容許的誤差值,需要分析泰勒式中的餘項。
線性化的使用
穩定性分析
在自治系統的穩定性分析中,可以使用在雙曲平衡點評估的雅可比矩陣的特徵值來確定該平衡的性質。這是線性化定理的內容。
個體經濟學
在個體經濟學中,決策規則可以線上性化的狀態空間方法下近似。
最佳化
在數學最佳化中,成本函式和內部的非線性分量可以線性化,以便套用諸如Simplex算法的線性求解方法。最佳化的結果可以更有效地得到全局最優的解 。
多物理學
在多物理場系統中,涉及多個彼此相互作用的物理場的系統,可以執行關於每個物理場的線性化。該系統關於每個場的線性化會形成線性化的單片方程系統,其可以使用單片疊代解決方案如牛頓 - 拉夫遜(Newton-Raphson)方法來求解。這樣的例子包括機械和聲場系統的MRI掃瞄器系統等 。