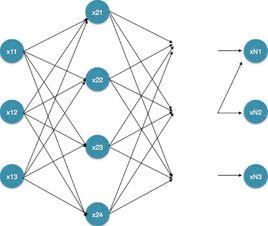
來源
維特比算法由安德魯·維特比(Andrew Viterbi)於1967年提出,用於在數字通信鏈路中解卷積以消除噪音。 此算法被廣泛套用於CDMA和GSM數字蜂窩網路、撥號數據機、衛星、深空通信和802.11無線網路中解卷積碼。現今也被常常用於語音識別、關鍵字識別、計算語言學和生物信息學中。例如在語音(語音識別)中,聲音信號作為觀察到的事件序列,而文本字元串,被看作是隱含的產生聲音信號的原因,因此可對聲音信號套用維特比算法尋找最有可能的文本字元串。
算法
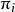 維特比算法
維特比算法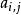 維特比算法
維特比算法 維特比算法
維特比算法 維特比算法
維特比算法假設給定隱式馬爾可夫模型(HMM)狀態空間 S,共有k個狀態,初始狀態i的機率為 ,從狀態 i 到狀態 j 的轉移機率為 。 令觀察到的輸出為 。 產生觀察結果的最有可能的狀態序列 由遞推關係給出:
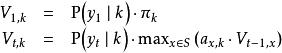 維特比算法
維特比算法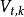 維特比算法
維特比算法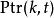 維特比算法
維特比算法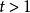 維特比算法
維特比算法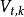 維特比算法
維特比算法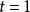 維特比算法
維特比算法此處 是前 t 個最終狀態為 k 的觀測結果最有可能對應的狀態序列的機率。 通過保存向後指針記住在第二個等式中用到的狀態 x 可以獲得維特比路徑。聲明一個函式 ,它返回若 時計算 用到的 x 值 或若 時的 k,這樣:
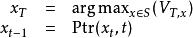 維特比算法
維特比算法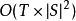 維特比算法
維特比算法這裡我們使用了arg max的標準定義 算法複雜度為 。
算法基礎
維特比算法的基礎可以概括成下面三點:
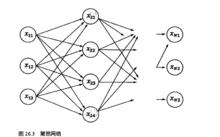 數學之美維特比算法
數學之美維特比算法1.如果機率最大的路徑p(或者說最短路徑)經過某個點,比如途中的X,那么這條路徑上的起始點S到X的這段子路徑Q,一定是S到X之間的最短路徑。否則,用S到X的最短路徑R替代Q,便構成一條比P更短的路徑,這顯然是矛盾的。證明了滿足最優性原理。
2.從S到E的路徑必定經過第i個時刻的某個狀態,假定第i個時刻有k個狀態,那么如果記錄了從S到第i個狀態的所有k個節點的最短路徑,最終的最短路徑必經過其中一條,這樣,在任意時刻,只要考慮非常有限的最短路即可。
3. 結合以上兩點,假定當我們從狀態i進入狀態i+1時,從S到狀態i上各個節的最短路徑已經找到,並且記錄在這些節點上,那么在計算從起點S到第i+1狀態的某個節點X的最短路徑時,只要考慮從S到前一個狀態i所有的k個節點的最短路徑,以及從這個節點到X,j的距離即可。