基本介紹
圖1是一個維恩圖解的例子，其中兩個事件(A和B)是獨立的。這兩個事件是相互排斥的，不可能同時發生，所以兩個圓圈沒有相互重疊。圓圈所在的區域表示為P(A)和P(B)，事件A和B發生的機率 。
圖1兩個相互排斥的事件A和B的維恩圖解你可以把維恩圖解看成是箭靶子。構想朝這個靶子放出一枝箭，這枝箭落在靶子上任何區域的機率都是相等的，但是一定會擊中這個靶子。靶子上的圓圈代表每一個可能的事件，所以如果射出的箭落在了圓圈A，就代表了事件A發生了。再進一步， 每一個圓圈所在區域大小代表該區域每一個事件發生的機率。其目的是將每一個圓圈代表的區域與每一個事件的機率相對應，但是通常很難(這裡也沒有做到)做到。在圖1中，我無法將一枝箭同時射中A和B，所以，這兩個事件不可能同時發生。
現在必須介紹一些其他的符號;
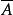維恩圖解(讀作A槓)表示事件A將不會發生。
(A∪B) (讀作A聯合B)表示事件A和B至少有一個發生。
(A∪B) 在維恩圖解中是圓圈A和圓圈B覆蓋的區域，而A∩B是一般指圓圈A和圓圈B共同覆蓋的區域。在圖1中，事件A和B是相互排斥的，舉例來說，可以看到:
P(A∪B)= P(A)+ P(B)； (1)
P(A∩B)=0；
維恩圖解
圖2 不相互獨立的兩個事件A和B的維恩圖解現在看看圖2，A和B不是相互排斥的:它們可以同時發生，在維恩圖解中用重疊代表。這個圖中產生了四種不同的區域。可以從以下區域觀察到：
P(A∪B)= P(A)+P(B)-P(A∩B)， (2)
P(A∩B)= P(A)P(B) 在A和B相互獨立時，或者
P(A∩B) = P(A)P(B/A) 在A和B不相互獨立時 。
例題解析
【例1】對於更為複雜的問題，維恩圖解變得非常有用。如果一隻綿羊可能患A、B、C和D疾病中的一種，機率分別為12%、8%、7%和2%。如果患任何一種疾病，都不能通過檢驗檢疫。A、B和C三種疾病相互之間是獨立的，但是疾病D不可能與疾病A、B或者C同時發生，原因是引起疾病D的寄生蟲無法存活。任何一隻特定的綿羊不能通過檢疫檢驗的機率P(F)是多少?使用圖3，通過計算區域並去除重複計算的區域可以得到：
P(F)=P(A∪B∪C)+P(D)
=P(A)+P(B)+ P(C)-P(A∩B)-P(A∩C)-P(B∩C)+P(A∩B∩C)+P(D)
= 0.267
所以，條件機率如何適合維恩圖解?這一點可以非常容易地通過例子說清楚 。
圖3 例1的維恩圖解【例2】我們現在想像投擲硬幣三次。事件A是第一次投擲得到正面，事件B是第二次游投擲得到正面，事件C是最少有一次投擲得到正面，事件D是所有投擲都得到正面。圖4畫出了這個問題的維恩圖解。
圖4 例2的維恩圖解有8種可能的結果:
結果1：TTT
結果2：HTT
結果3：THT
結果4：TTH
結果5：HHT
結果6：THH
結果7：HTH
結果8：HHH
上面定義的事件由以下結果組成：
A={2，5，7，8}
B= (5，6, 8}
C={2,3,4,5,6,7,8}
D={8}
這些結果展示在維恩圖解之中。由於對於一個平衡的硬幣來講，每一個結果都具有相同的機率，我們就可以看到：
P(A)=1/2
P(B) =1/2
P(C)=7/8
P(D)=1/8
我們看看機率P(A/B)=p (第一次投擲=H|第二次投擲=H)。結果(3，5，6，8}全部都在事件B中，但是只有{5，8}也在事件A中。這樣，P(A/B)=P({5，8})/P({3，5, 6，8})=1/2。對於一個平衡的硬幣而言，由於每次投擲是獨立的，這也就是我們知覺所期望得到的結果。這個例子說明在維恩圖解中，條件機率P(A/B)就是區域B同時包含在區域A中的比例 。
