概述
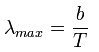其數學表示為維恩位移定律（Wien's displacement law）是物理學上描述黑體電磁輻射能流密度的峰值波長與自身溫度之間反比關係的定律，其數學表示為：
式中式中：
為輻射的峰值波長（單位米），
為黑體的絕對溫度（單位開爾文），
b 為比例常數，稱為維恩位移常數，數值等於2.897 7685(51) × 10–3 m K （2002年國際科技數據委員會(CODATA)推薦值，括弧中為68.27%置信度下的不確定尾數）。
光學上一般使用納米（nm）作為波長單位，則 b = 2.897 7685(51) × 106 nm K.
定義
維恩位移定律維恩位移定律闡明黑體輻射場的能量密度取極大值處的波長同熱力學溫度之間關係的定律。這個定律和維恩公式（見普朗克公式）的建立，是W.維恩對黑體輻射理論的發展作出的重要貢獻。
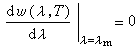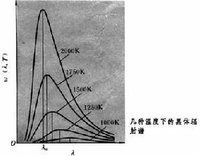
維恩位移定律根據黑體輻射的普朗克公式，輻射能量密度w(λ,T)在波長λm處有極大值，λm滿足方程
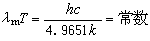維恩位移定律，用數值法對此式求解，可得
,式中h、k、和 с分別為普朗克常數、玻耳茲曼常數和真空中的光速。可見，對應輻射場密度極大值的波長（最可幾波長）λm同熱力學溫度 T的乘積為恆量。最可幾波長同溫度成反比。溫度升高，λm向短波方向移動；溫度愈高，能量愈集中在高頻區。這就是維恩位移定律（見圖）。 由於輻射通量密度同輻射能量密度之比為с/4,這樣，測出對應輻射通量密度極大值的λm，就可根據上式確定輻射體溫度。套用這個原理可製成光測高溫計（見高溫計）。
說明問題
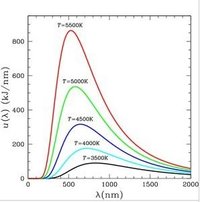維恩位移定律維恩位移定律說明了一個物體越熱，其輻射譜的波長越短（或者說其輻射譜的頻率越高）。譬如在宇宙中，不同恆星隨表面溫度的不同會顯示出不同的顏色，溫度較高的顯藍色，次之顯白色，瀕臨燃盡而膨脹的紅巨星表面溫度只有2000-3000K，因而顯紅色。太陽的表面溫度是5778K，根據維恩位移定律計算得的峰值輻射波長則為502nm，這近似處於可見光光譜範圍的中點，為黃光。
與太陽表面相比，通電的白熾燈的溫度要低數千度，所以白熾燈的輻射光譜偏橙。至於處於“紅熱”狀態的電爐絲等物體，溫度要更低，所以更加顯紅色。溫度再下降，輻射波長便超出了可見光範圍，進入紅外區，譬如人體釋放的輻射就主要是紅外線，軍事上使用的紅外線夜視儀就是通過探測這種紅外線來進行“夜視”的。
本定律由德國物理學家威廉·維恩（Wilhelm Wien）於1893年通過對實驗數據的經驗總結提出。
頻率形式
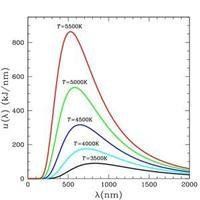用f 表示頻率，單位赫茲，則維恩位移定律可表示為以下頻率形式用f 表示頻率，單位赫茲，則維恩位移定律可表示為以下頻率形式。
(完整公式見右圖 圖一）
是數值求解最大值方程得到的常數； k 為玻爾茲曼常數， h a~~2.821439為普朗克常數，
T 為絕對溫度（單位開爾文）
需要注意的是，以上頻率形式中的輻射能流密度定義為“通過單位面積、單位寬度的頻率帶在單位時間中輻射出的能量”，而波長形式的輻射能流密度則定義為“通過單位面積、單位寬度的波長範圍在單位時間中輻射出的能量”，因此fmax和λmax對應的並不是同一個輻射峰。所以 fmax和波長形式中的 λmax不滿足 頻率×波長=波速 的關係式，即：(公式見右圖 圖二）
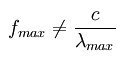頻率×波長=波速 的關係式，即：其中c 表示光速。
定律的推導
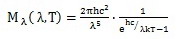普朗克黑體輻射公式雖然威廉·維恩提出本定律的時間是在普朗克黑體輻射定律出現之前的1893年，且過程完全基於對實驗數
據的經驗總結，但可以證明，本定律是更為廣義的普朗克黑體輻射定律的一個直接推論。
根據普朗克定律，以波長為自變數的黑體輻射能流密度譜為：
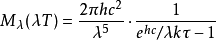維恩位移定律為求出使得 M取得最大值的λ，令M(λ)對λ 的導數為0
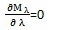微分方程若定義無量綱（又稱“無因次”）變數
則
方程的解無法表示成初等函式（為郎伯W函式），但能否得到精確解並不影響本推導過程。可以很容易用數值方法得到x
(無量綱) 將解代入x 的表達式，可得：
. 其中λ單位為納米，溫度單位為開爾文。
本定律的頻率形式也可通過類似的方法推得，只要將作為出發點的普朗克定律寫成頻率形式即可。
利用普朗克黑體輻射公式中的M對 λ微分，令其為零，可得 λ=b/T,即為證明過程。
注釋
^ 可見光顏色的波長從長到短依次為紅->橙->黃->綠->青->藍->紫 ^ 整個太陽光光譜完整復蓋（且超出）了可見光光譜範圍，使得太陽光（在沒有大氣的情況下）呈白色。至於人們在地上所看見的紅日、藍天等現象，都是由於大氣層氣體分子對短波長光線作瑞利散射（Rayleigh scattering）的結果。
定律的套用
維恩位移定律有許多實際的套用，例如通過測定星體的譜線的分布來確定其熱力學溫度；也可以通過比較物體表面不同區域的顏色變化情況，來確定物體表面的溫度分布，這種以圖形表示出熱力學溫度分布又稱為熱象圖。利用熱象圖的遙感技術可以監測森林防火，也可以用來監測人體某些部位的病變。熱象圖的套用範圍日益廣泛，在宇航、工業、醫學、軍事等方面套用前景很好。
