基本介紹
隨機過程
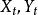 純隨機過程
純隨機過程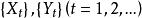 純隨機過程
純隨機過程由隨機變數組成的一個有序序列,或一個隨機變數按照時間編排的集合,稱為隨機過程(stochastic process)。記作;或。
時間序列
隨機過程的一次觀測結果稱為時間序列。記法同上。
隨機過程或時間序列一般分為兩類:一類是離散型的,一類是連續型的。
白噪音(聲)
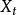 純隨機過程
純隨機過程若一個隨機時間序列是一個具有零均值同方差,而且不存在序列相關,即
 純隨機過程
純隨機過程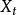 純隨機過程
純隨機過程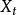 純隨機過程
純隨機過程則稱序列是一個 白噪音或 白噪聲(white noise)過程,即 純隨機過程(purely random process)。如果序列是獨立同分布的,則稱之為 嚴格白噪音(strictly white noise) 。
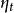 純隨機過程
純隨機過程當一個隨機過程包含隨機變數,其相互獨立同分布(independentand identically distribution),則該隨機過程被稱為 純隨機過程(purely random)。它暗指該過程有同定的均值和方差,純隨機過程始終是平穩過程。
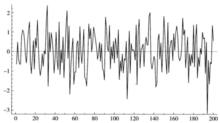 圖1
圖1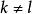 純隨機過程
純隨機過程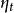 純隨機過程
純隨機過程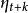 純隨機過程
純隨機過程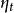 純隨機過程
純隨機過程另外,對於純隨機過程的與的自相關係數為零。圖1包含一個樣本數為N=200的常態分配的隨機過程的實例。檢查可觀測時間序列是否為隨機過程的重要診斷工具是相關分析圖。圖1中的殘差數據的前12階相關分析圖如圖2所示。隨機過程變數的獨立性應當反映為所有自相關係數近似等於零。
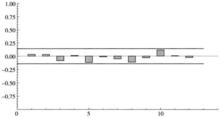 圖2
圖2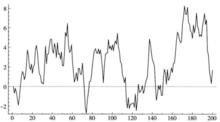 圖3 隨機遊走
圖3 隨機遊走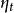 純隨機過程
純隨機過程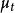 純隨機過程
純隨機過程令為純隨機過程,則為隨機遊走(random walk)的形式化定義為:
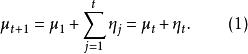 純隨機過程
純隨機過程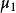 純隨機過程
純隨機過程數值為未知。如果服從式(1),則隨機遊走的一階差分等於:
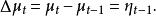 純隨機過程
純隨機過程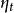 純隨機過程
純隨機過程 純隨機過程
純隨機過程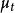 純隨機過程
純隨機過程隨機遊走的一階差分為平穩隨機過程。如果我們用圖1中的的數值,以及利用公式1計算的數值,我們得到如圖3所示的時間序列。在圖3清楚地指出,隨機遊走並不是平穩過程,因為序列的均值隨著時間變化。圖4顯示了圖3中的序列的相關分析圖,圖4的自相關的模式是典型的非平穩過程:自相關係數只有在非常大的滯後階數才接近於零 。
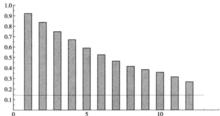 圖4
圖4平穩過程
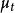 純隨機過程
純隨機過程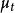 純隨機過程
純隨機過程 純隨機過程
純隨機過程 純隨機過程
純隨機過程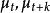 純隨機過程
純隨機過程 純隨機過程
純隨機過程當一個隨機過程的均值、方差和自協方差不隨時間變化,其被稱為 二階平穩(second-order stationary)或者 弱平穩(weakly stationary)過程。自協方差隨著相應的滯後而變化。與自相關類似,自協方差是序列與序列自身向後平移K個時點的協方差。序列平穩的屬性指不管序列的時間點在哪裡,只要其問距相等,的協方差就相同。注意當,則協方差就簡化為方差 。