約翰-威廉斯模型的內容
為簡化起見，約翰和威廉斯模型只考慮全權益公司。在期初公司內部管理者確定了投資額I，然後根據投資額選擇股利發放額D,I和D所需資金要么來自公司的現金C，要么來源於新股發行PcN 介入（為Pc 每股除息後價格，N為新股發行數）。從而有：
D + I = C + PcN （1）
以上四個因素不存在信息不對稱問題，無論內部人員還是外部人員都能獲得這些信息。但是，現有資產或投資項目產生的未來現金流屬於私人信息，只有內幕人員才知道，外部人員對只有一個主觀的機率分布。
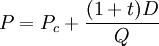約翰-威廉斯模型假設所有股東都是同質類型的，股利所得稅率為t，增發新股前的外發股票數量為Q，如果不存在無風險套利機制，則每股除息前的價格為P為：
公司現有股東的現金需求主要通過兩個渠道來滿足：（1）股利，（2）賣出一部分股票，其計算公式為:
L = D + PcM （3）
式中：M為賣出股票的數量(M<Q)。
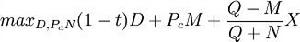約翰-威廉斯模型現有股東的現金流入量包括三部分，即稅後股利，出售股票所得和股權稀釋後仍能享受的部分公司剩餘權益。內部管理者的目的是使股東財富最大化，其計算公式為：
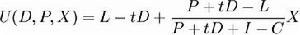約翰-威廉斯模型將式(1)至(3)代入(4)式，並記U表示現有股東的現金流入量，則可得
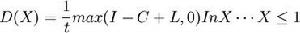約翰-威廉斯模型經過整理求微分後，可解出在有效信號均衡條件下的最優股利為：
約翰和威廉斯模型信號均衡是遞耗式的，如果沒有稅或遞耗成本(發放股利而增收的股利所得稅)，信號均衡就不存在。而且由於稅的存在，在發放股利時，同時會發放新股，從而造成股權稀釋。
約翰和威廉斯模型認為，在信號均衡時，內部管理者的目標是尋求現有股東財富最大化，所要做的決策是股利，新股發行和投資支出三個。股利支付的決策要考慮分配股利所能得到的邊際效益，當公司投資及股東個人的現金需求大於公司內部的現金供給時，則發放股利會產生較多的有利信號，二級市場上股價會上升，所需發行新股的數量就減少，股權稀釋程度就小，加之股價的溢價，可以彌補收到的股利所要交納的稅負。如果資金需求小於供給，股利的發放產生的有利信號就少，發放股利就要考慮股利的遞耗成本和稀釋股權所得到的邊際利益之間的權衡。
約翰和威廉斯模型解決了為什麼公司會以稅收的代價來發放現金股利，但缺陷是難以解釋為什麼投資者一定要通過出售股票來滿足資金需要，而不通過負債或其他融資手段，因為其它方式的成本甚至更低。
參考文獻
1 徐明聖.股利信號理論模型及其套用[J].金融教學與研究,2002,(6)
相關條目
巴恰塔亞模型
米勒-羅克模型
約翰—威廉斯模型
