定義
按公式定義
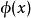 算數階層
算數階層 算數階層
算數階層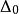 算數階層
算數階層 算數階層
算數階層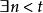 算數階層
算數階層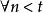 算數階層
算數階層 算數階層
算數階層設 為自然數的語言中的公式,定義 為 公式若且唯若 中的所有量詞都是有界量詞(即形如 或 的量詞,其中 為該語言中的項)。
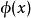 算數階層
算數階層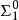 算數階層
算數階層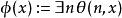 算數階層
算數階層 算數階層
算數階層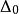 算數階層
算數階層 算數階層
算數階層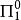 算數階層
算數階層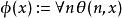 算數階層
算數階層 算數階層
算數階層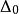 算數階層
算數階層定義 為 公式若且唯若 ,其中 為 ;定義 為 公式若且唯若 ,其中 為 。
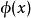 算數階層
算數階層 算數階層
算數階層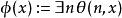 算數階層
算數階層 算數階層
算數階層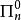 算數階層
算數階層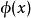 算數階層
算數階層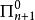 算數階層
算數階層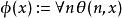 算數階層
算數階層 算數階層
算數階層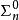 算數階層
算數階層更進一步定義 為 公式若且唯若 ,其中 為 公式;定義 為 公式若且唯若 ,其中 為 公式。
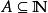 算數階層
算數階層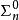 算數階層
算數階層 算數階層
算數階層 算數階層
算數階層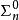 算數階層
算數階層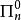 算數階層
算數階層 算數階層
算數階層 算數階層
算數階層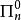 算數階層
算數階層 算數階層
算數階層 算數階層
算數階層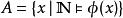 算數階層
算數階層 算數階層
算數階層 算數階層
算數階層設 ;若存在 公式定義 則稱 為 集合,若存在 公式定義 則稱 為 公式。(若有公式 與集合 ,使 ,則稱 定義 。)
按可計算性定義
 算數階層
算數階層 算數階層
算數階層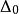 算數階層
算數階層 算數階層
算數階層 算數階層
算數階層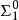 算數階層
算數階層 算數階層
算數階層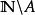 算數階層
算數階層 算數階層
算數階層若集合 可以用圖靈機(或任何等價的計算模型)計算得出,則稱 為 集合。若 為遞歸可枚舉集合則稱 為 集合,若 的補集 遞歸可枚舉則稱 為 集合。這一定義實際上與上面給出的定義是等價的。
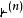 算數階層
算數階層 算數階層
算數階層 算數階層
算數階層 算數階層
算數階層 算數階層
算數階層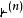 算數階層
算數階層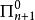 算數階層
算數階層更高階層的算術類可以通過波斯特定理與可計算性聯繫起來:設 為零不可解度的第 次圖靈跳躍,則任何集合 是 集合若且唯若 可以用具備 的預言機遞歸枚舉;任何集合是 集合若且唯若其補集滿足以上條件。
舉例
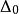 算數階層
算數階層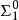 算數階層
算數階層所有遞歸集合都是 集合、所有遞歸可枚舉集合都是 集合(逆命題亦成立)。
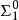 算數階層
算數階層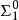 算數階層
算數階層停機集合(即所有停機的圖靈機)是 集合,它在 類中是完全的。
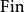 算數階層
算數階層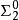 算數階層
算數階層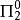 算數階層
算數階層所有有限遞歸可枚舉集合的編號(記作 )是 -完全集合(因此所有無限遞歸可枚舉集合的編號是 -完全集合)。
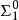 算數階層
算數階層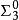 算數階層
算數階層所有 -完全集合作為遞歸可枚舉集合的編號是 -完全集合。
可計算性理論
在計算機科學中, 可計算性理論(Computability theory)作為計算理論的一個分支,研究在不同的計算模型下哪些算法問題能夠被解決。相對應的,計算理論的另一塊主要內容,計算複雜性理論考慮一個問題怎樣才能被有效的解決。
