定義
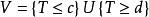 等尾檢驗
等尾檢驗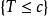 等尾檢驗
等尾檢驗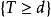 等尾檢驗
等尾檢驗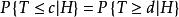 等尾檢驗
等尾檢驗稱雙側檢驗為對稱的,如果在H成立的條件下,事件和有相同的機率:。
原理
對稱性是客觀世界的一個本質屬性,對稱的條件勢必導致結論的對稱(此結論通常被稱為不充足理由律),利用這種對稱原理可以輔助我們的決策。如果經濟周期是對稱的,那么可以從經濟周期擴張期的性質來對比經濟周期收縮期的性質,可以從經濟周期峰頂的性質來推斷經濟周期谷底的性質。在經濟周期擴張期採用的制止經濟過熱的經濟收縮政策,可以在經濟收縮期改變其政策方向,進而作為擴張政策來促使經濟回升。經濟周期的對稱性意味著經濟政策作用的對稱性,經濟政策的擴張和收縮在方向上可以順周期和反周期調控經濟運行;如果經濟周期是對稱的,那么一些體現經濟周期特徵的主要巨觀經濟變數的時間序列也是對稱的,因此可以利用線性時間序列模型進行描述,因為線性變換不會改變原來時間序列和機率分布的對稱性。
對稱性無比簡潔和深刻,在人類思維上同樣有著深刻的反映,利用對稱性原理,許多思維上的難題可以迎刃而解。比如,肯定一個結論往往很困難,每一個充分條件都要證明;但從其對稱面否定一個結論常常又非常容易,只需要否定其一個必要條件即可,所以,在人們日常的思維活動中,往往通過對結論的否定來引導出肯定結論,或者說,是通過對許多假象的排斥來導出要證實的結論。如果說,對稱性是人腦智慧的極重要的方法特性,那么它也應該是探討人工智慧的一個極重要的工具,就如同要診斷患者患什麼病,往往不是直接得出判定結論,而是在排斥諸多可疑疾病後,才可得出患某種病的結論。
在決策中,人們也往往是在否定了諸多方案之後才得以肯定一個最佳方案。決策,就是“作出決定”,“拍板”。當然不是盲目地拍板。決策是為了達到一定的目標,從兩個或兩個以上的可行方案中選擇一個合理方案的分析判斷的過程。西蒙說:系列決策組成的;管理就是決策。”“決策是管理的心臟;管理是由一決策對於組織的重要性不言而喻。決策的正確與否,決定著組織行為的成敗。正確的決策,能指導組織沿著正確的方向、合理的路線前進;錯誤的決策,就會使組織走上錯誤的道路,可能導致組織的失敗、消亡。對稱檢驗就是要從反面去考慮。當我們在做決策時,還要考慮反決策。對於一個方案的好壞不妨從對稱性出發進行分析,對方案所會產生的利弊的結果都要進行研討,充分考慮此方案可能產生的各種影響,不要只看到好的一面,還要看到不好的一面;不只考慮上此項目,還要考慮不上此項目不僅從同類相似方案中選優,還要進行對稱方案的比較。
比如,對於是否要修一個大型水電站的決策,我們不僅要看到修建的好處:發電,抗洪等;同時也考慮到可能會帶來的不利影響:如對於生態的影響等,要比較建與不建的利弊,要進行方案優選,還要進行大、小方案,大、中方案的比較。經過充分論證之後,在我們實施決策時,就會心中有數,所以儘量做到趨利避害。
我們對於某項決策相關的信息的了解和掌握不可能窮盡。只進行可行性研究,而不從對稱性出發進行不可行性研究,就使得原本“殘缺”的信息出現了嚴重的不對稱——影響決策的正、反兩方面信息的不對稱。信息不對稱就談不上客觀全面,出現誤導在所難免。在可行性研究的基礎上(或同時)進行不可行性研究,即所謂“兼聽則明”,專門對決策實施方案的可行性“雞蛋裡面挑骨頭”,尋找潛在的、隱藏的問題和風險,可以使決策信息趨於平衡,給決策者提供更廣闊的思路和的信息,以利全面、準確地權衡利弊得失,提高決策的科學性。即使不可行研究最終不被採用,但是它仍然具有借鑑意義,可以起到警示作用,有利於決策在實施過程中更大程度地減少失誤,規避風險。如果說進行可行性研究相比個別領導拍腦袋是一大進步,那么運用對稱性同時進行不可行性研究,則比只進行可行性研究更進了一步。
相關概念
雙尾檢驗
雙尾檢驗是考慮分布的兩端,無論是正態曲線分布,均值抽樣分布,差異抽樣分布,或其他任何分布。在雙尾檢驗中,我們不預測觀察數據落在抽樣分布的什麼地方,一個負的t值和正的t值一樣,因為我們考察的是抽樣分布的兩端。總之,我們對分布於兩側都感興趣的時候,雙尾檢驗變成了單尾檢驗或者是我們不要求在實驗開始前做任何的猜測。
單尾檢驗
單尾檢驗只考慮抽樣分布的一端。對於其預測,研究者應該有一個好的解釋,最好是基於之前的研究、事實證據或邏輯的解釋。因為,如果預測成真以及實驗結果是在期望的方向,只考慮分布的一端或一尾的單尾檢驗是一個更強有力的檢驗。我們說更強有力,意思是指在同一個顯著水平下,查表所得單尾檢驗中達到顯著水平的值比雙尾檢驗中達到顯著水平的值要小。例如,雙尾檢驗無限自由度下的5%水平臨界值是1.960。而對於單尾檢驗,相應的臨界值是來自10%的列.按照這個指示,單尾檢驗將百分比減小了一半。因此,單尾檢驗無限自由度下5%水平的臨界值是1.6449。
但是用單尾檢驗有一個危險。請記住,我們必須在做研究前對實驗結果做一個預測。如果我們的預測是錯誤的,並且在平均數檢驗上觀察到一個與預測結果方向相反的一個很大的差異呢?因為我們使用單尾檢驗時著眼於錯誤的一邊,我們將無法拒絕零假設.使用雙尾檢驗將會允許拒絕。換句話說,只有在我們的預測準確時,雙尾檢驗才是一個更強有力的檢驗。因為這個原因,也因為實驗者傾向於在數據輸入後為單尾檢驗做一個合理的解釋,許多統計學家反對以任何理由使用單尾檢驗。我們的立場是,如果我們可以在數據收集前合理地預測結果的方向,那么使用一個更敏感的檢驗是有保障的。如果我們能對我們的數據合理的使用單尾檢驗,那么我們將降低一半的機率值在表B中確定t檢驗的臨界值。