定義
第一數學歸納法可以概括為以下三步:
(1)歸納奠基:證明n=1時命題成立;
(2)歸納假設:假設n=k時命題成立;
(3)歸納遞推:由歸納假設推出n=k+1時命題也成立.
從而就可斷定命題對於從所有正整數都成立。
數學歸納法的正確性證明:
假設我們已經完成下面的推理
歸納基礎:P(0)真;
歸納推理:對於任意k (P(k)→P(k+1))
但是還並非所有自然數都有性質P。
將這些不滿足性質P的自然數構成一個非空自然數子集,這樣,子集中必定有一個最小的自然數,設為m。
顯然m>0,記做n+1,這樣n一定具有性質P,即P(n)為真
存在n(P(n)∧¬P(n+1))╞╡對於任意的k(¬P(k)∨P(k+1))不滿足╞╡對於任意的k(P(k)→P(k+1))不滿足
假設推理結果與已經完成的歸納推理矛盾,所以假設錯誤。
所有自然數都有性質P。
例子
假設我們要證明下面這個公式():
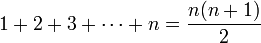
其中 n 為任意自然數。這是用於計算前 n 個自然數的和的簡單公式。證明這個公式成立的步驟如下。證明
第一步是驗證這個公式在 n = 1 時成立。我們有左邊 = 1,而右邊 = 1(1 + 1) / 2 = 1,所以這個公式在 n = 1 時成立。第一步完成。
第二步
第二步我們需要證明如果假設n = m 時公式成立,那么可以推導出 n = m+1 時公式也成立。證明步驟如下。
我們先假設 n = m 時公式成立。即
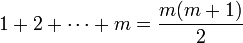
然後在等式等號兩邊分別加上 m + 1 得到
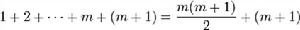
這就是 n = m+1 時的等式。我們現在需要根據等式 1 證明等式 2 成立。通過因式分解合併,等式 2 的右手邊
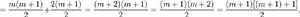
也就是說
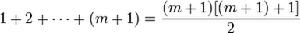
這樣便證明了從 P(m) 成立可以推導出 P(m+1) 也成立。證明至此結叢,結論:對於任意自然數 n,P(n) 均成立。
