積分梳狀濾波器原理
積分梳狀濾波器（CIC）結構簡單高效，不需要進行乘法運算，可以對高速數據流進行低通濾波運算。下面以CIC抽取濾波器為例進行分析。設抽取因子為D，則單級濾波器的衝激回響具有如下形式：
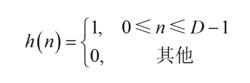積分梳狀濾波器（2.100）
其傳遞函式為：
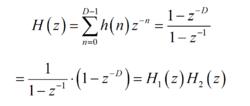積分梳狀濾波器（2.101）
式中，
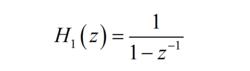積分梳狀濾波器（2.102）
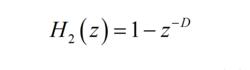積分梳狀濾波器（2.103）
由式（2.101）可以看出，CIC濾波器由積分單元H（z）和梳狀單元H（z）級聯組成。單級CIC抽取濾波器如圖1所示。
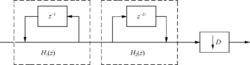積分梳狀濾波器圖1單級CIC抽取濾波器
利用Noble恆等式，可以得到其等效結構如圖2所示。
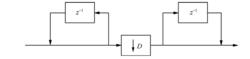積分梳狀濾波器圖2單級CIC抽取濾波器等效結構
該等效結構使梳狀單元工作在較低的採樣率下，因此是實際採用的實現形式。
令z=e ，分別計算積分單元和梳狀單元的頻率回響如下：
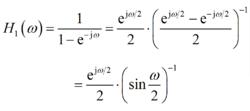積分梳狀濾波器（2.104）
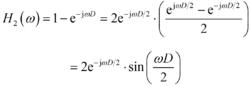積分梳狀濾波器（2.105）
可以看出，梳狀單元的幅頻特性為H（w）=2|sin（wD/2）|，具有梳齒的形狀，這也是其名稱的來由。濾波器總的頻率回響為：
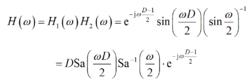積分梳狀濾波器（2.106）
CIC濾波器並非理想低通濾波器，其頻率回響有旁瓣電平的存在。單級CIC濾波器的旁瓣電平較大。例如較大時第一旁瓣的電平為：
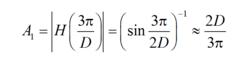積分梳狀濾波器（2.107）
與D比較：
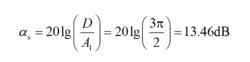積分梳狀濾波器（2.108）
為了降低旁瓣電平，可以採用多級CIC濾波器級聯的辦法來解決。N級級聯的CIC濾波器幅頻回響為：
積分梳狀濾波器（2.109）
主瓣與旁瓣電平相比，
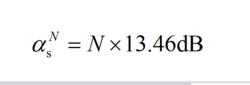積分梳狀濾波器（2.110）
N越大，旁瓣抑制得越好。但是，增大後，通帶內的平坦度會變差，因此也不宜太多，一般以5級為限。級聯CIC濾波器的實現框圖如圖3所示。
積分梳狀濾波器圖3級聯CIC抽取濾波器
同樣，可以利用CIC濾波器實現內插過程，級聯結構如圖4所示。
積分梳狀濾波器圖4級聯CIC內插濾波器
