稀疏表示
現有稀疏表示模型一般形式如下:
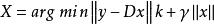 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法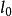 稀疏表示分類法
稀疏表示分類法其中,y 為觀測數據, D 為字典, x 為待估稀疏向量,
為正則參數, k (1≤ k<2 )為稀疏度量。其中,與 k 未知, 需要預先確定( 雖然通常取 k =1 , 但 k <1 時模型更加靈活)。對該模型的理論研究, 主要包括模型解與範數最小化解的逼近程度、 稀疏表示模型解的唯一性與穩定性等。但是, 在一些具體的套用如圖像增強與測控資源最佳化配置中, 稀疏度量並不是唯一且最重要的指標。
模型求解算法
 稀疏表示分類法
稀疏表示分類法上述模型的求解劃分為基於數學模型的求解算法, 如基追蹤、 FOCUSS 、Shrinkage 等, 以及不考慮數學模型的求解算法, 如匹配追蹤算法族等。但現有的算法多存在一個待解決問題, 即需預先確定正則參數與表征稀疏度的參數 k , 然後進行求解。若解未達到要求, 則重新調整兩個參數的值, 直至得到滿意解。這使得模型在套用中不能達到自動化的程度,限制了稀疏表示方法的套用。
字典學習算法
最初在稀疏表示研究領域, 一般假定字典已知, 僅求解未知稀疏向量。現已有學者研究字典的選擇與學習方法用於字典未知的情況。現有的字典學習方法可分為兩種類型: 基於訓練樣本與基於參數化字典 。其中, 後者較為困難, 需深入分析所研究的信號的特點與描述方法。對字典學習的過程一般採用兩步法, 與稀疏表示模型求解相結合。
信號稀疏表示套用
目前, 稀疏表示的套用範圍基本為自然信號形成的圖像、音頻以及文本等, 對於非自然信號或數據的套用尚未有文獻涉及。在套用方面, 可大體劃分為兩類:
基於重構的套用
此類套用有圖像去噪、 壓縮與超分辨 、SAR 成像 、 缺失圖像重構以及音頻修復 等。這些套用主要將目標的特徵用若干參數來表示,這些特徵構成稀疏向量,利用稀疏表示方法得到稀疏向量,根據數學模型進行數據或圖像重構。在這些套用中,觀測數據一般含有噪聲。
基於分類的套用
這類套用的本質是模式識別 , 將表征對象主要的或本質的特徵構造稀疏向量, 這些特徵具有類間的強區分性。利用稀疏表示方法得到這些特徵的值, 並根據稀疏向量與某類標準值的距離, 或稀疏向量間的距離判別完成模式識別或分類過程, 例如盲源分離、 音樂表示與分類、人臉識別、文本檢測。
稀疏表示分類(SRC)
假定有來自 c 個類的 n 個訓練樣本,其中,有足夠的訓練樣本屬於第 k 類 ,
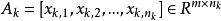 稀疏表示分類法
稀疏表示分類法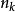 稀疏表示分類法
稀疏表示分類法其中,m 是訓練樣本的維度, 是屬於第 k 個類的訓練樣本的個數。
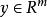 稀疏表示分類法
稀疏表示分類法來自第 k 類的任何測試樣本 可以近似表示為該類的訓練樣本的線性組合
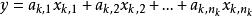 稀疏表示分類法
稀疏表示分類法由於y的標籤最初是未知的,我們將y表示為所有訓練樣本的線性組合:
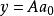 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法其中, ,是由c個類的所有n個訓練樣本組成的矩陣;
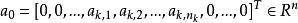 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法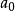 稀疏表示分類法
稀疏表示分類法,是係數向量,僅與之相關聯的第 k個類的係數是非零的。 當 大時, 會很稀疏。
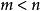 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法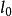 稀疏表示分類法
稀疏表示分類法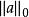 稀疏表示分類法
稀疏表示分類法如果 ,則上式的求解式不確定的。稀疏表示的問題就是尋找一個滿足上式條件的向量 ,並且, 的 範數—— 是最小的。這可以表示為:
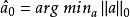 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法然而,找到上式的稀疏解是NP-hard :即,現階段沒有比窮舉a的所有子集更有效的獲得稀疏解的方法。 稀疏表示和壓縮感知理論 揭示了我們可以解決以下凸最佳化,以獲得近似解:
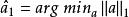 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法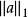 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法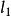 稀疏表示分類法
稀疏表示分類法其中, 是 的 範數。這個問題可以通過標準的線性規劃方法來解決。此外,觀察經常是不準確的,那么我們應該放鬆方程式的約束,並得到以下最佳化問題:
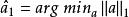 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法其中, 是可容忍的誤差。這種凸最佳化問題可以通過二階錐規劃來解決。
最佳化問題(上式)主要用於處理小噪聲。 在實踐中,觀測結果可能含有較大的噪音。例如,圖像被損壞或遮擋,誤差不能被最佳化問題忽略或解決。 約束應修改為
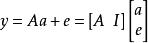 稀疏表示分類法
稀疏表示分類法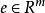 稀疏表示分類法
稀疏表示分類法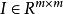 稀疏表示分類法
稀疏表示分類法其中, 是誤差矩陣, 是單位矩陣。現在,我們得到以下最佳化問題:
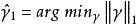 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法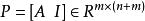 稀疏表示分類法
稀疏表示分類法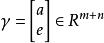 稀疏表示分類法
稀疏表示分類法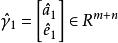 稀疏表示分類法
稀疏表示分類法其中, , ,
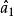 稀疏表示分類法
稀疏表示分類法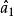 稀疏表示分類法
稀疏表示分類法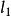 稀疏表示分類法
稀疏表示分類法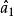 稀疏表示分類法
稀疏表示分類法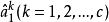 稀疏表示分類法
稀疏表示分類法令表示通過最小化 範數獲得的稀疏表示問題的解。 理想情況下,中的非零元素將與單個對象類中的列有關,我們可以輕鬆地將測試樣本 y 分配給該類。 然而,噪聲和建模錯誤可能導致多個類與小的非零項相關聯。 諸如將y分配給具有最大非零項的類的簡單啟發式是不可靠的。 相反,我們定義一個新的向量,,其只有非零項是中與類別 k 相關聯的項。
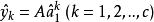 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法 稀疏表示分類法
稀疏表示分類法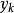 稀疏表示分類法
稀疏表示分類法第 k 類的訓練樣本的重建是, 那么可以將分配給和 之間的殘差最小的類:
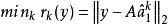 稀疏表示分類法
稀疏表示分類法SRC算法
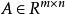 稀疏表示分類法
稀疏表示分類法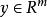 稀疏表示分類法
稀疏表示分類法1)輸入:訓練樣本的矩陣,測試樣本
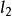 稀疏表示分類法
稀疏表示分類法2)規一化A的列,以使之具有單位 範數。
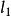 稀疏表示分類法
稀疏表示分類法3)解決上述方程式中定義的 最小化問題。
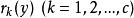 稀疏表示分類法
稀疏表示分類法4)計算殘差
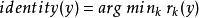 稀疏表示分類法
稀疏表示分類法5)輸出:
