運算元
運算元(英語:Operator)是從一個向量空間(或模)到另一個向量空間(或模)的映射。 運算元對於線性代數和泛函分析都至關重要,它在純數學和套用數學的許多其他領域中都有套用。 例如,在經典力學中,導數的使用無處不在,而在量子力學中,可觀察量由埃爾米特運算元表示。 各種運算元可以具有包括線性、連續性和有界性等的重要性質。
設U、V是兩個向量空間。 從U到V的任意映射被稱為 運算元。 令V是域K上的向量空間。我們可以定義包含所有從U到V運算元的集合上的向量空間結構(A和B是運算元):
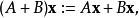 矩陣運算元
矩陣運算元 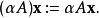 矩陣運算元
矩陣運算元  矩陣運算元
矩陣運算元  矩陣運算元
矩陣運算元 對所有A, B: U→V,x U和α K。從一個向量空間到自身的運算元構成一個辛結合代數:
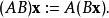 矩陣運算元
矩陣運算元 單位元是恆等映射(通常記為E、I或id)。
有界運算元和運算元範數
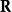 矩陣運算元
矩陣運算元 令U和V是同一有序域(例如 )上的兩個賦范向量空間。從U到V的線性運算元被稱為 有界,如果存在C>0滿足
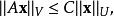 矩陣運算元
矩陣運算元  矩陣運算元
矩陣運算元 對所有x U。
有界運算元構成一個向量空間。在這個向量空間上,我們可以引入一個與U和V的範數相容的範數:
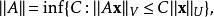 矩陣運算元
矩陣運算元 對於從U到自身的運算元有
 矩陣運算元
矩陣運算元 任何具有這一性質的辛賦范代數被稱為Banach代數。 可以將譜理論推廣到這樣的代數上。C*-代數是具有一些附加結構的Banach代數,在量子力學中起重要作用。
特殊情形
泛函
泛函是將向量空間映射到其底域的運算元。廣義函式理論和變分法是泛函的重要套用。 兩者對理論物理都非常重要。
線性運算元
線性運算元是最常見的運算元。設U和V是域K上的向量空間。運算元A:U→V被稱為線性,如果
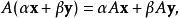 矩陣運算元
矩陣運算元  矩陣運算元
矩陣運算元  矩陣運算元
矩陣運算元 對所有x、y U和α、β K。線性運算元的重要性在於它是向量空間之間的態射。
 矩陣運算元
矩陣運算元 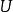 矩陣運算元
矩陣運算元 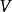 矩陣運算元
矩陣運算元  矩陣運算元
矩陣運算元 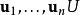 矩陣運算元
矩陣運算元  矩陣運算元
矩陣運算元 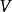 矩陣運算元
矩陣運算元 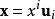 矩陣運算元
矩陣運算元 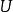 矩陣運算元
矩陣運算元 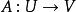 矩陣運算元
矩陣運算元 在有限維情形下,線性運算元可以以下面的方式由矩陣表示。 設 是一個域, 和 是 上有限維向量空間。選擇一組基 上和一組基 在 上。令 為 上的任意向量(假設有愛因斯坦求和約定),且有 是線性運算元。則有
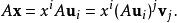 矩陣運算元
矩陣運算元 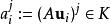 矩陣運算元
矩陣運算元  矩陣運算元
矩陣運算元 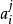 矩陣運算元
矩陣運算元  矩陣運算元
矩陣運算元 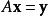 矩陣運算元
矩陣運算元 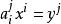 矩陣運算元
矩陣運算元 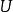 矩陣運算元
矩陣運算元 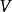 矩陣運算元
矩陣運算元 所以有 是運算元 在固定基底下的矩陣表示。 不依賴於 的選取,且有 若且唯若 。因此在固定基底下的n×m矩陣一一映射到從 到 的線性運算元。
與有限維向量空間之間的運算元直接相關的重要概念包括秩、行列式、逆運算元和特徵空間。
線性運算元在無限維情形也起著重要作用。秩和行列式的概念不能擴展到無限維矩陣。 這就是為什麼在無限維情況下研究線性運算元(和一般的運算元)時採用非常不同的技術的原因。 在無限維情況下的對線性運算元的研究被稱為泛函分析。
實數序列(或更一般地任意向量空間中的向量序列)的空間本身構成無限維向量空間。 最重要的情形是實數或複數序列,這些空間與線性子空間一起被稱為序列空間。 這些空間上的運算元被稱為序列變換。
巴拿赫空間上的有界線性運算元在標準運算元範數意義下構成Banach代數。 Banach代數理論將特徵空間理論推廣到更一般的譜的概念。
例子
幾何
在幾何中,有時研究向量空間上的附加結構。 在這些研究中,將這些向量空間一一映射到自身的運算元非常有用,它們通過構造自然地構成群。
例如保持向量空間結構的雙射運算元正是可逆線性運算元。 它們構成了一般線性群。 它們運算元加法下不是向量空間,例如,id和-id都是可逆的(雙射),但它們的和為0,不可逆。
在這樣的空間上保持歐幾里得度量的運算元構成等度群,保持原型不變的子群被稱為正交群。正交群中的保角運算元構成特殊正交群。
機率論
機率論中也涉及到運算元,如期望、方差、協方差、階乘等。
微積分
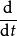 矩陣運算元
矩陣運算元 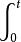 矩陣運算元
矩陣運算元 從泛函分析的角度來說,微積分是研究兩個線性運算元:微分運算元 和不定積分運算元 。
標量和向量場上的基本運算元
三個運算元是向量微積分的關鍵:
 矩陣運算元
矩陣運算元 Grad(梯度),(運算元符號 )在標量場中的每個點對應一個向量,指向該場最大變化率的方向,並且其範數是該最大變化率的絕對值。
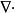 矩陣運算元
矩陣運算元 Div(散度),(運算元符號 )是一個向量運算元,用於描述向場從給定點向外的發散度或朝向給定點的收斂度。
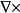 矩陣運算元
矩陣運算元 Curl(旋度),(運算元符號 )是一個向量運算元,用於描述在給定點的向量場旋轉程度。
作為從向量微積分運算元到物理、工程和張量空間的延伸,梯度、散度和旋度運算元也經常與張量微積分相關聯。
另請參閱
• 運算
• 函式
• 數學符號表
• 向量空間
• 對偶空間
• 運算元代數
• Banach代數
• 運算元列表
• 算符
• 運運算元(編程)
