簡介
在多感測器融合理論中，一般研究的是同步數據融合，即假設各感測器同步對目標進行測量，並且同步傳送到融合中心。而實際過程中，感測器系統存在不同觀測時間和數據傳輸延遲，人們將感測器系統分為同步感測器系統(SSTF)和異步感測器系統(ASTF)。在同步感測器系統中，對來自不同感測器的數據進行融合和噪聲平滑再送往融合中心，在異步多感測器系統中，需要將不同時刻的數據統一到融合中心同一時刻上，再對量測數據進行最佳化、融合。利用信息互補，通過數據融合技術，可以給出對目標位置的精確估計，改善對目標的跟蹤和識別。
算法概述
對異步感測器數據融合的方法主要有Alouani提出的基於量測和模型噪聲相互獨立的最優異步融合算法，Blair的最小二乘數據壓縮法以及異步航跡融合方法等。Alouani算法複雜，不容易工程實現，Blair模型需要大量數據，無法滿足實時、線上計算的要求，引用同步最優融合的加權方法，未構成誤差協方差跡最小的異步融合。並且，目前異步融合最主要的局限性在於各種算法都只能適用於兩兩感測器之間的異步融合，對來自於多個感測器的異步數據無法進行有效處理。
關鍵技術
雷達和紅外感測器是當前最常用的兩類主/被動探測手段。雷達可以獲得目標的完整位置信息，具有較好的測距、測速性能;紅外感測器可以提供高精度的目標角度信息和強的目標識別能力。
異類感測器數據融合的關鍵是進行異類感測器的數據關聯，即確定主被動感測器建立的航跡是否源於同一個目標。由於兩類感測器的工作機理不同，使得在異類感測器數據關聯中存在以下問題:①主被動感測器的數據率往往不一致，數據存在異步性。②紅外感測器僅有角度測量而沒有距離測量。③兩類感測器的測角精度相差較大，數據冗餘度大。
對於雷達和紅外數據融合，既可採用基於測量的集中式融合跟蹤，也可採用分散式處理方法，即首先由雷達和紅外各自建立關於目標的航跡，然後再進行雷達與紅外航跡的關聯和融合。從理論上講，基於測量的融合可以得到關於目標狀態的最優估計，分散式處理是次優的。
多感測器異步數據融合
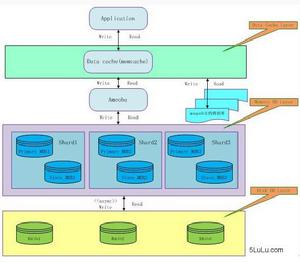
融合中心的採樣間隔T和相應的離散時間標記k不同於感測器節點的採樣間隔T和相應的離散時間標記k，如圖所示。
離散化後各感測器的濾波方程為
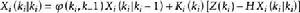異步數據融合
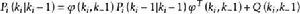異步數據融合
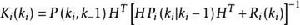異步數據融合
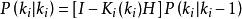異步數據融合我們可以假設融合中心的狀態估計值可以由各感測器節點的狀態估計值的線性組合來表示：
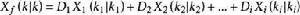異步數據融合對等式兩邊求期望:
異步數據融合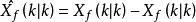
異步數據融合記誤差 的方差陣為P(k)，則其估計為:
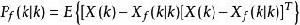異步數據融合假設感測器之間相互獨立，根據協方差矩陣跡最小原則有下式成立：
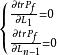異步數據融合對於兩兩配準的感測器，在下一式成立：
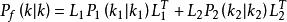異步數據融合令
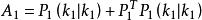異步數據融合
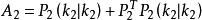異步數據融合則有
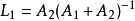異步數據融合
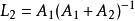異步數據融合對於多感測器系統，假設有n個感測器，設L為未知係數(注意無偏條件)，有n=N時
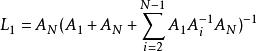異步數據融合
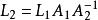異步數據融合...
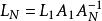異步數據融合
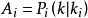異步數據融合由於各感測器的誤差協方差陣為對稱陣，在實際運算中可有
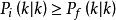異步數據融合對於同步模式下多感測器融合系統來說，應該有
同理，對於異步模式下多感測器融合系統則有
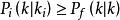異步數據融合雷達和紅外數據融合
雷達和紅外數據融合是典型的異類感測器數據融合，把雷達和紅外感測器組合使用構成雷達/紅外多感測器系統，能夠使系統降低對敵方干擾的脆弱性，提高系統可靠性;利用雷達高精度的距離測量和紅外感測器高精度的角度測量，利用信息互補，通過數據融合技術，可以給出對目標位置的精確估計，改善對目標的跟蹤以及提高系統的生存能力，因而引起了廣泛的注意。
在集中融合系統框架下，首先採用最小二乘法對測量數據實現同步化處理，接著利用角度信息進行主被動感測器數據關聯，最後根據各自的測角精度，對紅外與雷達角度數據賦予不同的權值，壓縮處理後得到相關融合後的角度信息，結合雷達距離信息作為最終的融合結果。
以雷達、紅外的多感測器目標跟蹤為技術特徵的異步數據融合研究，利用最小二乘法將異步數據同步化，提出了基於相似性測度分析的數據關聯算法，採用了基於測角精度的目標狀態信息壓縮算法。與最近鄰航跡關聯算法相比，相似性測度法的正確關聯機率要改善20%，數據處理量和存儲量都不大，便於套用。數學分析認為，航跡融合後的目標狀態數據精度不低於單個探測器的數據精度。仿真研究表明，融合紅外搜尋跟蹤裝置所產生的目標航跡信息後，雷達的角跟蹤精度得到了大幅度改善，這對於目標跟蹤誤差的減小具有重要的意義。
