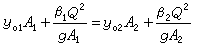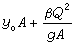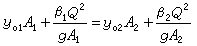瑞利－里茲法

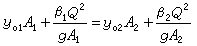
瑞利－里茲法，通過泛函駐值條件求未知函式的一種近似方法，是英國的瑞利於1877年在《聲學理論》一書中首先採用，後由瑞士的W.里茲於1908年作為一個有效方法提出。這一方法在許多力學、物理學問題中得到套用。

瑞利－里茲法

此法假定待求函式f(x)為n個已知函式 Wi(x)的線性組合：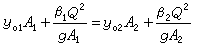

式中αi為未知常係數。通過由f(x)組成的泛函嗘【f(x)】取駐值的條件(駐值條件對應於已知的物理定律或定理)得到n個方程： 由此解出n個未知常係數αi,從而得到f(x)。這一理論還可推廣到多維問題。
在求解彈性體位移時,先假定彈性體內沿x、y、z方向的位移u、v、w 分別由一系列已知的滿足彈性體全部位移邊界條件的連續函式ui(x，y，z)、vi(x，y，z)、wi(x，y，z)(i=1，2，…，n)疊加而成，即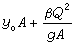

式中Ai、Bi、Ci為待求係數，共3n個。將u、v、w代入作為泛函的總勢能∏ 的表達式，根據彈性力學最小勢能原理，總勢能變分為零，即有駐值條件： 這是關於3n個待求係數Ai、Bi、Ci的3n個代數方程。解出3n個未知係數便得到全部位移。通過對位移進行微商並利用應力－應變關係就得到應力。由於瑞利－里茲法假設的位移函式u、v、w可以不滿足力的邊界條件,所以位移函式的構成比較容易,計算也比較方便,但有時求出的應力誤差較大。
在振動問題中，如果將物體的可能位移表達為若干給定的位移的線性組合，而以瑞利商（見瑞利原理）作為位移的泛函，則利用瑞利商取駐值的條件，就可求出物體振動的固有頻率的近似值。
參考書目
　鷲津久一郎著，老亮、郝松林譯：《彈性和塑性力學中的變分法》，科學出版社，北京，1984。(Kyuichiro Washizu,Variational　Methods in Elasticity　and Plasticity,2nd ed.,Pergamon Press,Oxford,1975.)

配圖

相關連線