二次量子化中的產生湮滅算符
波色場的產生湮滅算符
例如最簡單的無相互作用標量場
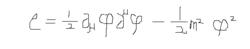湮滅算符.
二次量子化後，令
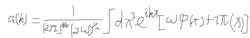湮滅算符其中π是廣義動量，則a與它的厄密共軛滿足關係式
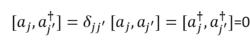湮滅產生算符對易關係其中，a的厄密共軛就叫產生算符。根據以上對易關係，任給一個量子態，不斷用產生算符作用在上面，總是能得到新的量子態，對於無相互作用的場論，同一個產生算符不管作用在哪一個量子態上，新的量子態增加的能量總是一定的，並且新的量子態的運動規律含有單粒子運動規律類似的成分。因此，就把產生算符的作用定義為產生了一個粒子。產生算符的名字由此而來。對應的a是湮滅算符，作用在有這個粒子的態上，消去一個粒子，作用在沒有這個粒子的態上結果為0.
費米場的產生湮滅算符
與玻色子不同的是，費米子的產生湮滅算符滿足反對易關係而非對易關係，這樣，重複產生一個粒子會得到0.正好與泡利不相容原理相符。
場論以外的產生湮滅算符
實際上，普通量子力學中也可以使用產生湮滅算符解決問題。這時，產生湮滅算符不再對應產生或者消去一個可以真實運動的粒子，而僅僅是某種量子。具體情況通常比場論中的產生湮滅算符簡單，他們都具有產生湮滅算符類似的對易（或反對易）關係。
