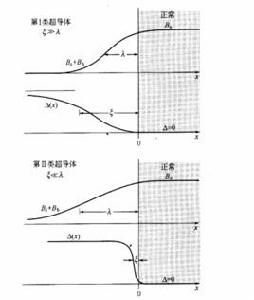
第一類超導體與第二類超導體的對比
第一類和第二類超導體的超導電性機制沒有差別。在零磁場中,兩類超導體在超導態-正常態轉變點處具有相似的熱學性質。但邁斯納效應完全不同。
 渦旋態
渦旋態 渦旋態
渦旋態 渦旋態
渦旋態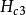 渦旋態
渦旋態好的第一類超導體完全排除磁場,直到超導電性被突然破壞,然後磁場完全穿透。好的第二類超導體完全排除磁場,直到磁場達到某 。在 以上,磁場被部分排除,但樣品仍保持超導性。在更強的場 下,磁通完全穿透,同時超導電性消失(樣品的一個外表面層可能保持超導,直到達到某群更高的場 )。
 穿透深度與相干長度與正常態傳導電子的平均自由程的關係
穿透深度與相干長度與正常態傳導電子的平均自由程的關係 渦旋態
渦旋態 渦旋態
渦旋態 渦旋態
渦旋態第一類同第二類超導體間的一個重要差別是正常態傳導電子的平均自由程的差別。如果相干長度 比穿透深度 大,超導體將是第一類。大多數純金屬是第二類超導體,因為 。但是,如果平均自由程短,相干長度短,穿透深度大,則超導體將是第二類。
通過適量地摻人一種合金元素,能夠把某某些金屬從第一類變為第二類。在鉛中加入2%(質量)的鋼,能使鉛從第一類變為第二類,雖然轉變溫度幾乎一點也不變。這種摻雜性的合金化對鉛的電子結構沒有本質影響,但在超導態下的磁性行為發生劇烈變化。
第二類超導體的理論是Ginzburg、Laudau、Abrikosov和Gorkov提出來的,後來Kunzler及其合作者觀測到NbSn線在接近100kG的磁場下能負載大的超導電流,這推動了強場超導磁體的商業化開發。
考慮一個超導區域與一個正常區域之間的界面,界面具有表面能,可以是正的或者是負的,而且隨外磁場的增強而減小。如果表面能總是正的,則超體是第一類;如果當磁場增加表面能變負,則是第二類超導體。表面能的正負對於轉變溫度沒有重要影響。
渦旋態的由來
 渦旋態
渦旋態當磁場被排出,塊體超導體的自由能增加,但是縱向(平行於膜的方向)的磁場能幾乎均勻地穿透很薄的膜,只有一部分磁通被排出。同時,隨著外磁場的增強,超導膜的能量僅緩慢地增加。這就使破壞超導電性所需的磁場強度大為提高。膜具有通常的能隙,並且將是無電阻的。薄膜不是第二類超導體,但關於膜的研究結果表明:在適當的條件下超導電性能夠在高磁場下存在。
 由SEM對Nb3Se2在1000G和0.2K下得到的磁通晶格圖樣
由SEM對Nb3Se2在1000G和0.2K下得到的磁通晶格圖樣關於薄膜結果提出這樣一個問題:是否存在超導體在磁場中的穩定結構,其體內有些區域是正常態的細棒(或平板)形式,每個正常區都被超導區所包圍?在這種被稱之為渦旋態的混合態中,外磁場將均勻地穿透薄的正常區,而且磁場也將或多或少傳進周圍的超導材料當中。
 渦旋態
渦旋態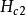 渦旋態
渦旋態渦旋態一詞描述貫穿整個塊體樣品的渦旋形式的超異電流環流。在渦旋態下,正常區同超導區之間沒有化學上的或晶體學上的差別。因為外場穿透進入超導材料,使表面能變為負,所以渦旋態是穩定的。在一定的磁場範圍內即 和 之間,保持穩定的渦旋態是第二類超導體的特徵。
形成渦旋態的條件
 渦旋態
渦旋態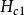 渦旋態
渦旋態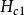 渦旋態
渦旋態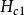 渦旋態
渦旋態隨著外加磁場的增強,形成渦旋態的起始條件是什麼呢?根據穿透深度 ,我們可以估算 。如果外加磁場為 ,那么在包含磁通量子的正常區核中的磁場應該是 。
 渦旋態
渦旋態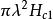 渦旋態
渦旋態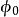 渦旋態
渦旋態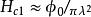 渦旋態
渦旋態從正常核向外擴展一個距離 ,進入周圍的超導區,這樣與單個核相聯繫的磁通是 ,它必須等於磁通量子 。由此(1),這是單個磁通量子的成核場。
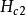 渦旋態
渦旋態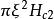 渦旋態
渦旋態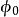 渦旋態
渦旋態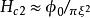 渦旋態
渦旋態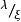 渦旋態
渦旋態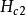 渦旋態
渦旋態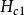 渦旋態
渦旋態在 下,磁通量子儘可能緊密地排在一起以保持超導態的條件,這意味著如相干長度所容許的那樣儘可能密集。外場幾乎均勻地貫穿樣品,只是有微小的波動起伏,其尺度可與磁通量子晶格相比擬,每個核負載數量級為的磁通 ,後者也應量子化為 。因此(2),給出上臨界場,比值 愈大,對 比 值也就會愈大。
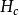 渦旋態
渦旋態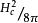 渦旋態
渦旋態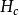 渦旋態
渦旋態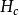 渦旋態
渦旋態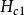 渦旋態
渦旋態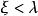 渦旋態
渦旋態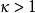 渦旋態
渦旋態我們還要尋求這些臨界場與熱力學臨界場 之間的關係。 量度超導態的穩定能密度,該密度是 。對於第二類超導體,只能用量熱法測量穩定能,以間接地確定 。為了通過 估計 ,應該考慮在絕對零度非純極限 下渦旋態的穩定性。這時 ,並且相干長度比穿透深度短。
 渦旋態
渦旋態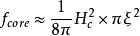 渦旋態
渦旋態我們估計在渦旋態下磁通量子核的穩定能,這核看作是負載著平均磁場 的正常金屬圓柱體。半徑的數量級是相干長度,即正常同超導相之間邊界厚度。參照於純超導體的能量,正常核(每單位長度)的能量由穩定能與核面積的乘積給出:(3)。
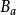 渦旋態
渦旋態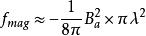 渦旋態
渦旋態但是由於外場 穿透到核周圖的超導材料內,所以磁能降低:(4)。
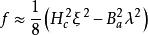 渦旋態
渦旋態對於單個的磁通量子,可將以上這兩項相加,從而得到:(5)。
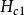 渦旋態
渦旋態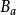 渦旋態
渦旋態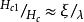 渦旋態
渦旋態當f<0時,核就是穩定的。根據定義,穩定磁通量子的閾場是在f=0時的場。用表示 ,則有(6)。
閾場把表面能為正的區域同表面能為負的區域分開。
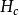 渦旋態
渦旋態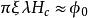 渦旋態
渦旋態合併式(1)和(6)得到關於的一個關係式:(7)。
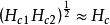 渦旋態
渦旋態還可以合併式(1),(2)和(6)得到:(8)
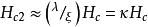 渦旋態
渦旋態和(9)。