簡介
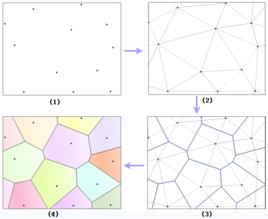
 泰森多邊形
泰森多邊形從幾何角度來看,兩基站的分界線是兩點之間連線的鉛直等分線,將全平面分為兩個半平面,各半平面中任何一點與本半平面內基站的間隔都要比到另一基站間隔小。當基站數量在二個以上時,全平面會劃分為多個包羅一個基站的區域,區域中任何一點都與本區域內基站間隔最近,是以這些個區域可以看作是基站的覆蓋區域,我們將這種由多個點將平面劃分成的圖稱為泰森多邊形,又稱為Voronoi 圖。
泰森多邊形的特性
1、每個泰森多邊形內僅含有一個離散點數據;
2、泰森多邊形內的點到相應離散點的距離最近;
3、位於泰森多邊形邊上的點到其兩邊的離散點的距離相等。
泰森多邊形可用於定性分析、統計分析、鄰近分析等。例如,可以用離散點的性質來描述泰森多邊形區域的性質;可用離散點的數據來計算泰森多邊形區域的數據;判斷一個離散點與其它哪些離散點相鄰時,可根據泰森多邊形直接得出,且若泰森多邊形是n邊形,則就與n個離散點相鄰;當某一數據點落入某一泰森多邊形中時,它與相應的離散點最鄰近,無需計算距離。
在泰森多邊形的構建中,首先要將離散點構成三角網。這種三角網稱為Delaunay三角網。
泰森多邊形的建立步驟
建立泰森多邊形算法的關鍵是對離散數據點合理地連成三角網,即構建 Delaunay三角網。建立泰森多邊形的步驟如下:
1、離散點自動構建三角網,即構建 Delaunay三角網。對離散點和形成的三角形編號,記錄每個三角形是由哪三個離散點構成的;
2、找出與每個離散點相鄰的所有三角形的編號,並記錄下來。這隻要在已構建的三角網中找出具有一個相同頂點的所有三角形即可;
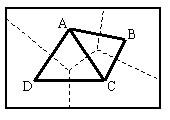
3、對與每個離散點相鄰的三角形按順時針或逆時針方向排序,以便下一步連線生成泰森多邊形。排序的方法可如圖所示。設離散點為o。找出以o為頂點的一個三角形,設為A;取三角形A除o以外的另一頂點,設為a,則另一個頂點也可找出,即為f;則下一個三角形必然是以of為邊的,即為三角形F;三角形F的另一頂點為e,則下一三角形是以oe為邊的;如此重複進行,直到回到oa邊;
4、計算每個三角形的外接圓圓心,並記錄之;
5、根據每個離散點的相鄰三角形,連線這些相鄰三角形的外接圓圓心,即得到泰森多邊形。對於三角網邊緣的泰森多邊形,可作垂直平分線與圖廓相交,與圖廓一起構成泰森多邊形。
參考
泰森多邊形的建立