熱力學
熱力學中的比贊數 是熱傳不可逆性和總不可逆性（因為熱傳及流體摩擦力）之間的比例：
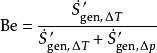比贊數其中
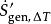比贊數是因為熱傳產生的熵，
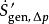比贊數是因為流體摩擦力產生的熵。
流體力學、熱傳學及質傳學
比贊數流體力學的比贊數是沿著長度管道的無因次壓力差：
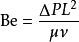比贊數其中
比贊數為粘度
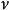比贊數是動量擴散率（運動粘度）
比贊數熱傳學的比贊數是沿著長度 管道的無因次壓力差：
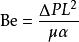比贊數其中
比贊數是粘度
比贊數是熱擴散率
比贊數在強制對流中的角色和瑞利數在自然對流中的角色相近。
質傳的比贊數是沿著長度的管道無因次壓力差：
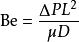比贊數其中
比贊數是粘度
比贊數是質傳擴散率
若在雷諾類比（英語：Reynolds analogy）的條件下（Le=Pr=Sc= 1），以上三種Bejan數都相同。
阿瓦德（Awad）和拉赫（Lage）提出了另一個修改版的比贊數，最早是從巴塔查爾吉（Bhattacharjee）和格羅赫德勒（Grosshandler）針對動量過程的研究所產生的，這種比贊數中不使用粘度，而用流體密度和動量擴散率的乘積來代替。此作法一方面更接近物理特性，而且此無因次量可以不受粘度影響。這種簡化也可以將比贊數延伸到其他的擴散過程中，例如熱傳，只要更換擴散係數即可。因此也可以產生通用的比贊數，描述壓力差和擴散之間的關係。已證明此通用形式對於符合雷諾類比（英語：Reynolds analogy）（Le=Pr=Sc= 1）的過程，會有類似的結果，也就是表示動量、能量及特定物質質量的比贊數會是相同的值。
因此，比贊數更中性的定義如下：
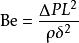比贊數其中
比贊數流體密度
比贊數為要考慮過程的擴散係數
此外，阿瓦德比較哈根數（英語：Hagen number）及流體力學的比贊數，兩者的物理意義是不同的，哈根數是無因次的壓力梯度，而比贊數是無因次的壓力差。不過若哈根數的特徵長度（l）等於比贊數的流體長度（L）， 因此在哈根-泊肅葉流中的比贊數可以用下式來定義
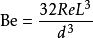比贊數其中
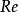比贊數為雷諾數
比贊數為流體長度
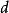比贊數為管路直徑
此處的比贊數也是無因次量。
