背景
該問題的出現是因為我們沒有同等程度的看待各個特徵，即我們沒有將各個特徵量化到統一的區間。比如對房屋售價進行預測時，我們的特徵僅有房屋面積一項，但是，在實際生活中，臥室數目也一定程度上影響了房屋售價。下面，我們有這樣一組訓練樣本（圖一）：
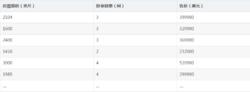圖一注意到，房屋面積及臥室數量兩個特徵在數值上差異巨大，如果直接將該樣本送入訓練，則代價函式的輪廓會是“扁長的”，在找到最優解前，梯度下降的過程不僅是曲折的，也是非常耗時的（圖二）：
圖二常用方法
Standardization
Standardization又稱為Z-score normalization，量化後的特徵將服從標準常態分配：
歸一化特徵
歸一化特徵其中，u和分別為對應特徵的均值和標準差。量化後的特徵將分布在[-1, 1]區間。
Min-Max Scaling
Min-Max Scaling又稱為Min-Max normalization， 特徵量化的公式為：
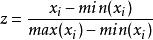歸一化特徵量化後的特徵將分布在區間。
大多數機器學習算法中，會選擇Standardization來進行特徵縮放，但是，Min-Max Scaling也並非會被棄置一地。在數字圖像處理中，像素強度通常就會被量化到[0,1]區間，在一般的神經網路算法中，也會要求特徵被量化[0，1]區間。
進行了特徵縮放以後，代價函式的輪廓會是“偏圓”的，梯度下降過程更加筆直，收斂更快性能因此也得到提升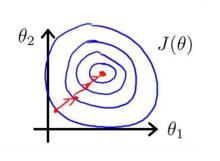（圖三）：
圖三