研究意義
正實性是系統控制研究的重要概念之一,自產生以來,就在穩定性研究與系統理論領域起著重要作用,它已廣泛套用於魯棒性分析、自適應控制和非線性系統的絕對穩定和超穩定等方面。控制系統的魯棒性問題一直是當今控制理論研究的熱點之一,比較起來,魯棒穩定性的研究比性能魯棒性的研究要多、要深入。實際系統不僅要求魯棒穩定,還要求系統具有一定的魯棒性能。如何研究系統的魯棒性能問題也是當今控制理論需要迫切解決的問題。正實性在系統和控制理論中的有關穩定性分析,超穩定性,自適應控制,二次性最優與代數黎卡提方程以及系統的穩定實現等方面都有很重要的意義。所以,研究正實控制具有重要意義。
發展
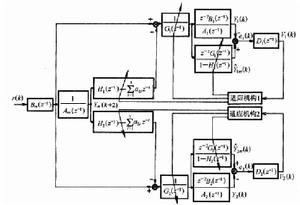
綜合內穩且閉環傳遞函式正實的問題稱為正實控制問題。對於正實控制問題的研究有大量的相關文章,正實控制問題的解可通過解黎卡提方程或不等式得到。討論狀態反饋和輸出反饋實現閉環系統的正實性問題,給出了正實控制問題的可解條件和基於解黎卡提方程或不等式構造控制器的方法。對狀態矩陣和輸入矩陣帶有不確定性的系統討論了魯棒正實控制問題,給出了動態輸出反饋的閉環系統魯棒穩定且嚴格正實的條件,證明了魯棒控制問題可轉化為確定系統的正實條件。解決了線性中立時滯系統的H∞控制和正實控制問題,並發展了相應的控制器的設計方案。
基於觀測器的正實控制即設計一個基於觀測器的控制器,使得閉合迴路系統是內穩且正實的。對不確定連續系統考慮了基於觀測器的正實控制問題。給出了基於觀測器的動態輸出反饋控制器的存在條件和求法。研究了基於觀測器的線性中立時滯系統的H∞控制,給出了控制器存在的充分條件及相應設計方案。有的文獻在原有的基礎上進一步研究該系統在不確定性更具一般性時的基於觀測器的正實性控制問題,此系統為一類線性不確定系統,該系統大量出現於經濟管理、電子網路、機器人、工業生產過程、生物過程和航天航空以及航海技術等領域,具有廣泛的實際背景。所以對這類系統進行正實控制,無論是對魯棒穩定性理論的進一步完善還是對解決實際問題都起著重要作用。
正實性
正實性是系統控制研究的重要概念之一,自產生以來,就在穩定性研究與系統理論領域起著重要作用,它己廣泛套用於魯棒性分析、自適應控制和非線性系統的絕對穩定和超穩定等方面。控制系統的魯棒性問題一直是當今控制理論研究的熱點之一,比較起來,魯棒穩定性的研究比性能魯棒性的研究要多、要深入。實際系統不僅要求魯棒穩定,還要求系統具有一定的魯棒性能。正實性在系統和控制理論中的有關穩定性分析、超穩定性、自適應控制、二次性最優與Riccati方程以及系統的穩定實現等方面都有很重要的意義。
綜合內穩定且閉環傳遞函式正實的問題稱為正實控制問題。對於正實控制問題的研究有大量的相關文章,正實控制問題的解可通過解Riccati方程或不等式得到,狀態控制和輸出反饋實現閉環系統的正實性也得到了研究,並給出了正實控制問題的可解條件和基於Riccati方程或不等式構造控制器的方法。對狀態矩陣和輸入矩陣帶有不確定性的系統討論了魯棒正實控制問題,給出了動態輸出反饋的閉環系統魯棒穩定且嚴格正實的條件,證明了魯棒控制問題可化為確定系統的正實條件。解決了線性中立時滯系統的控制和正實控制問題,並發展了相應的控制器的設計方案。
正實性定義如下:
(1)系統G(s)稱為正實的(PR),如果G(s)在開右半平面解析,且
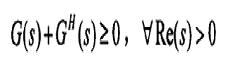 正實控制
正實控制(2)系統G(s)稱為嚴格正實的(SPR),如果G(s)在閉右半平面解析,且
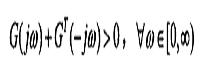 正實控制
正實控制(3)系統G(s)稱為擴展嚴格正實的(ESPR),如果G(s)嚴格正實,且
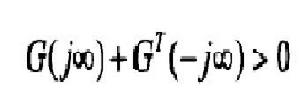 正實控制
正實控制正實控制
正實控制概念是從一類耗能電網中抽象出來的,是控制理論中的一個重要概念。眾所周知,絕對穩定性和超穩定性都與正實性密切相關,絕對穩定性和超穩定性等價於某線性環節的正實性。正實性在自適應某些算法的收斂性分析中起著關鍵作用。自適應系統本質上是時變的和非線性的,正實性定理是分析自適應系統尤其是高階系統穩定性的一個不可或缺的工具。另外,正實性在魯棒控制、非線性系統設計中也發揮著越來越重要的作用。若一個系統由嚴格正實環節和具有無源性的不確定環節或非線性環節或反饋互聯而成,則這個反饋系統是穩定的。這一事實為魯棒控制和非線性控制提供了一條重要的途徑。除此之外,正實性和界實性之間也存在緊密聯繫,它們之間可以互相轉化。由於有界實引理是H∞控制的基礎,正實性原理也為H∞控制提供了一種思路。綜上所述,研究系統的正實性和正實控制具有重要意義。
在時域中研究正實控制的理論基礎是正實引理,早期所用的方法是Riccati不等式或Riccati方程方法。很多文獻在這方面做出了有代表性的工作,討論了狀態反饋和輸出反饋實現閉環系統的正實問題,給出了正實控制問題的可解條件和基於Riccati不等式或Riccati方程構造控制器的方法。正實控制問題的Riccati方法可以給出控制器的結構,也便於理論分析。但具體實施時需要設計者預先確定一些特定參數,這些參數的選擇不僅影響到結論的好壞,而且還會影響到問題的可解性。現有的Riccati方法中還缺乏尋找這些參數最佳值的方法。參數的這種人為確定方法給綜合結果帶來了很大的保守性。另外,Riccati型矩陣方程本身的求解還存在一定的問題。現今很多求解Riccati方程的方法採用多位疊代法,收斂性不能得到保證。上世紀末,隨著求解凸最佳化問題的內點法的提出,線性矩陣不等式受到控制界的關注並被套用到正實控制領域,正實控制問題的線性矩陣不等式方法就產生了。基於線性矩陣不等式的正實控制問題的求解方法在計算機上是簡單可行的且它對系統的要求非常少。採用線性矩陣不等式處理方法解決正實控制問題,方法有兩種。一種是消去法:首先將閉環系統參數矩陣表示成控制器參數矩陣的仿射形式,然後根據正實引理寫出Lyapunov函式矩陣Xc,和控制器參數矩陣K的線性矩陣不等式,最後再解這個不等式,即先用雙邊投影定理消去K得到只含Xc的矩陣不等式,經過線性化處理求得Xc ,再將Xc,帶回原不等式得到只含K的線性矩陣不等式,從而可以利用求解線性矩陣不等式的方法得到控制器參數矩陣K。二是變數替換法:使用變數替換法需要先寫出閉環參數矩陣,根據正實引理寫出線性矩陣不等式,然後引進一組新的矩陣變數將這個非線性矩陣不等式化為新變數之間的線性矩陣不等式,再解線性矩陣不等式得到這組新變數的值,最後根據新舊變數之間的關係求得原變數的值,直至求得控制器參數的值。
另一方面,由於對系統缺乏足夠的了解,人們很難精確描述系統,有時系統本身比較複雜,人們也會根據需要簡化。因此,模型誤差是難免的。除了建模誤差,環境變化、器件老化、某些物理參數漂移等因素也會導致模型的不確定性。這樣在正實設計中一個不可迴避的問題是如何設計控制器使得閉環系統對所有允許不確定性都是正實的,這就是魯棒正實控制問題。另外由於時滯現象普遍存在,時滯系統經常在實際工程問題中出現,而時滯又常使系統失穩和性能惡化,時滯線性系統的H∞控制和正實控制問題十幾年來一直是人們研究的熱點。
所以針對上述問題,有的研究學者提出採用攝動參數多項式加範數有界攝動不確定模式,來描述進而研究實際系統的魯棒正實性分析與正實控制器的設計問題。由於攝動參數可以是時變的,這種不確定性模式可反映實際系統的時變特徵;而該不確定性模式中的範數有界攝動部分,可反映實際系統的不確定因素和被簡化掉的非線性特徵。從理論上看,這種不確定模式是傳統參數不確定性模型的自然推廣,它包含了現有的區間系統和範數有界攝動模型為其特例,這是對現有參數不確定模式的豐富和完善。