正交投影運算元

正交投影運算元是把任一元映到該元的正交投影的運算元，是希爾伯特空間上特別重要的一類運算元。

簡介

正交投影運算元是把任一元映到該元的正交投影的運算元。

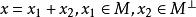正交投影運算元

設M是希爾伯特空間H的閉線性子空間，對任意x∈H，必有分解，定義運算元P如下：Px=x，即Px是x在M上的投影，稱運算元P為由H到M上的正交（或直交）投影運算元，簡稱投影（或射影）運算元。

性質

投影運算元P具有下列性質：

p =P（冪等）；

P有界（事實上有‖P‖=1）；

對一切x,y∈H,(Px,y)=(x,Py)成立（自伴）。反之，H上有界自伴的冪等運算元必是投影運算元。

正交投影運算元與H的閉線性子空間之間成一一對應。

滿足PQ=0的兩個正交投影運算元P和Q稱為相互正交的，記為P⊥Q。

套用

正交投影運算元是希爾伯特空間上特別重要的一類運算元，它是希爾伯特空間的很好的幾何特徵的反映，又是研究其他複雜運算元的工具。