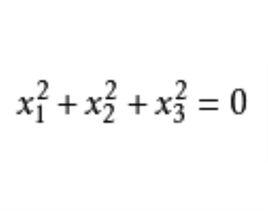基本介紹
 橢圓運動群
橢圓運動群設在復射影平而上給定零曲線C: 那么就有一個重要的定理。定理 如果C是零曲線,是射影平面上任意兩點,那么就有兩個而且只有兩個關於C的自同構把點a變成點a',並把通過a的任意已知的方向變為通過a'的任意已知的方向 。關於零曲線C的自同構稱為 橢圓射影運動,這時零曲線C就是橢圓運動的絕對形。具有公共絕對形的橢圓射影運動的全體構成的群,稱為 橢圓運動群。橢圓運動群的幾何稱為 橢圓幾 何,橢圓幾何就是黎曼幾何,這裡不作證明了。因為在橢圓幾何里絕對形是一個零曲線,所以,射影平面上的點都是橢圓幾何的點,射影平面上的直線都是橢圓幾何的直線。任何二直線的交點(指實的)都不在絕對形上,所以橢圓幾何里是沒有平行直線的 。
相關介紹
雙曲運動群與橢圓運動群
對於任意給定的空間S和該空間到自身的某個變換群G,如果群G中的變換g把空間S中一個點集U變到U自身,則稱g是關於點集U的自同構變換,簡稱為自同構。自同構可以變動點集U的點,但它必須把集合U的每個點還變成這個集合的點。
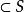 橢圓運動群
橢圓運動群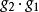 橢圓運動群
橢圓運動群若變換群G的兩個變換都是關於點集U()的自同構,則其乘積也是關於U的自同構;若g是G中關於U的自同構,則其逆變換也是關於U的自同構,因此,變換群G中關於U的自同構之全體構成N個變換群,稱為關於U的自同構群,它是G的子群。
例如,若在射影平面上任取一條直線,約定叫做無窮遠直線(記作),則射影變換群中關於的自同構之全體構成射影變換群的子群,即仿射變換群。又如,射影變換群中關於兩個圓點所成集合的自同構之全體構成射影變換群的子群,即相似變換群。
 橢圓運動群
橢圓運動群 橢圓運動群
橢圓運動群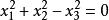 橢圓運動群
橢圓運動群 橢圓運動群
橢圓運動群在射影平面上任取一條常態實二階曲線,且取的一個自配極三點形作為坐標三點形時,它的方程是,則射影變換群中關於的自同構之全體也構成射影變換群的子群.
 橢圓運動群
橢圓運動群 橢圓運動群
橢圓運動群我們把射影變換群中關於一條常態實二階曲線的自同構稱為雙曲射影運動,稱為絕對形,具有公共絕對形的雙曲射影運動的全體構成射影群的子群,稱為雙曲運動群,研究雙曲運動群下的不變性質的幾何稱為雙曲幾何。
 橢圓運動群
橢圓運動群 橢圓運動群
橢圓運動群我們把射影變換群中關於一條常態虛二階曲線的自同構稱為橢圓射影運動,稱為絕對形,具有公共絕對形的橢圓射影運動的全體構成射影群的子群,稱為橢圓運動群,研究橢園運動群下的不變性質的幾何稱為橢圓幾何 。