簡介
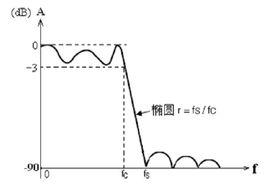
一個低通橢圓濾波器的頻率回響的幅度為:
四階低通橢圓濾波器的頻率回響。
其中Rn (x)是 n階雅可比橢圓函式(Chebyshev rational functions)。
特點介紹
從傳遞函式來看,巴特沃斯和切比雪夫濾波器的傳輸函式都是一個常數除以一個多項式, 為全極點網路, 僅在無限大阻帶處衰減為無限大. 而橢圓函式濾波器在有限頻率上既有零點又有極點。極零點在通帶內產生等波紋, 阻帶內的有限傳輸零點減少了過渡區, 可獲得極為陡峭的衰減曲線。也就是說在階數相同的條件下,橢圓濾波器相比於其他類型的濾波器,能獲得更窄的過渡頻寬和較小的阻帶波動, 就這點而言, 橢圓濾波器是最優的。它陡峭的過渡帶特性是用通帶和阻帶的起伏為代價來換取的,並且在通帶和阻帶的波動相同,這一點區別於在通帶和阻帶都平坦的巴特沃斯濾波器,以及通帶平坦、阻帶等波紋或是阻帶平坦、通帶等波紋的切比雪夫濾波器。
特點總結
1、橢圓低通濾波器是一種零、極點型濾波器,它在有限頻率範圍記憶體在傳輸零點和極點。
2、橢圓低通濾波器的通帶和阻帶都具有等波紋特性,因此通帶,阻帶逼近特性良好。
3、對於同樣的性能要求,它比前兩種濾波器所需用的階數都低,而且它的過渡帶比較窄。
但是橢圓濾波器傳輸函式是一種較複雜的逼近函式,利用傳統的設計方法進行電路網路綜合要進行繁瑣的計算, 還要根據計算結果進行查表, 整個設計, 調整都十分困難和繁瑣。而用MATLAB設計橢圓濾波器可以大大簡化設計過程。