簡介
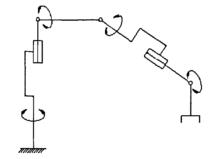機械手結構簡圖機械手可模仿人手和臂的某些動作，按固定程式實現抓取、裝配、搬運等動作。它是最早出現的工業機器人，可代替人的繁重勞動以實現生產的機械化和自動化，能代替人類完成危險作業。因此機械手廣泛套用於易燃易爆物品的裝配、搬運、拆卸、檢測，以及消防滅火、反恐防暴等高度危險的環境。
傳統的剛性機械手為獲得良好的定位精度，儘量增加機械手構件的剛度來減少振動。由於高精度機械手的操作性受限於機械手的動撓度，這樣導致定位工作滯後，機械手工作時能耗過大、運行速度低、負載能力差、驅動器的尺寸規格增大、成本增加等。為解決機械手操作的高速度與精確性的矛盾，柔性機械手應運而生。與傳統剛性機械手相比，柔性機械手具有質量輕、體積小、速度高、負載能力強、能耗小、成本低等優點。
長期以來，機器人手臂的動力學分析一直是難以很好解決的問題，主要表現在數學建模複雜，運算量大，難以實現實時控制等方面。這樣就限制了機器人的設計和套用性能，制約了精確的軌跡跟蹤。而動力學仿真軟體的套用無疑對提高機器人的設計性能、降低設計成本、減少產品開發時間提供了幫助，並為機械手的控制研究奠定了基礎。
目前，機器人手臂的動力學建模有很多種方法，最為常見的有基於Lagrange方程的方法、Kane方法、旋轉代數法和Newton—Euler方法等。仿真軟體也多種多樣，如ADAMS、DADS、DISCOOS等。其中基於Lagrange方程的建模方法以編程方便，可以直接與通用的商業軟體如ANSYS、ADAMS等對接而得到了廣泛套用。而且它不涉及約束力，直接建立主動力與運動的關係，在機器人系統動力學特性的分析上有明顯的優勢。
機械手動力學模型
拉格朗日函式L被定義為系統動能K和勢能P之差，即L=K-P
由拉格朗日函式L所描述的系統動力學狀態的拉格朗日方程為
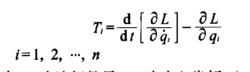機械手動力學式中：n為連桿數目；q為廣義坐標(m或rad)，q˙為廣義速度(m/s或rad/s)；T為作用在第i個坐標上的廣義力(N或N·m)。
機械手系統動能
系統動能等於各桿的動能之和。即系統的動能為
機械手動力學式中：J為偽慣性矩陣，即有
機械手動力學因此，n連桿的機械手總的動能為
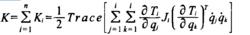機械手動力學
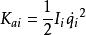機械手動力學則機械手連桿系統關節的傳動裝置總動能為
綜上，即得到機械手系統(包括傳動裝置)的總動能為
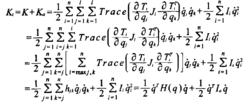機械手動力學
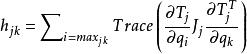機械手動力學式中：H(q)為機械手慣性矩陣，其中：；q和q˙為機械手關節轉角和角速度n維矢量；I為機械手關節傳動裝置等效傳動慣量矢量。
機械手系統勢能
系統勢能包括彈性勢能及重力勢能。
連桿i的勢能為
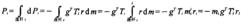機械手動力學在忽略傳動裝置重力情況下，機械手系統的總勢能為
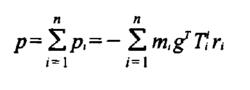機械手動力學式中：m為連桿i的質量，kg；r為連桿i相對於其前端關節坐標系的重心位置矢量；g 為重力加速度矢量。
柔性機械手動力學
與傳統剛性機械手相比，柔性機械手具有質量輕、體積小、速度高、負載能力強、能耗小、成本低等優點。柔性機械手的動力學特點是系統中的柔性部件在運動過程中經歷著大的剛體整體移動和轉動，同時又有變形運動，而且這兩種運動又是高度耦合的。剛性系統中，只要動參考系選定，質量矩陣等都是不隨時間變化的。但是在柔性系統中，包括質量矩陣等量都是隨著物體變形而變化，都是時間的函式，這使柔性機械手的動力學問題的複雜性大大增加。
柔性機械手的彈性來自機械手構件和關節的彈性。柔性機械手的數學模型中如果不考慮柔性就會影響所需電機轉矩和末端執行器位置的精確性。柔性機械手是一個複雜的動力學系統，其動力學方程具有高度非線性、強耦合、時變等特點，而進行柔性機械手動力學問題的研究，其模型的建立是極其重要的。
離散方法
柔性機械手是連續系統，可看作無數個多自由度，用一系列非線性耦合常微分和偏微分方程描述。它的精確動力學模型很難得到，因此通常將其離散成有限自由度作近似分析模型。為了便於分析計算，通常採用假定模態法(AAM)、有限元法(FEA)、集中質量法將其離散化。
假定模態法通常建立在Lagrange或Newton—Euler原理基礎上。它採用空間特徵方程和時變的模態幅度組成的有限個模態技術來描述彈性變形，採用模態截斷技術，利用系統中各個子結構的模態，綜合出系統的整個模態。Martins，Tso和MeteKalyoncu利用Lagrange方程和假定模態法研究了單桿柔性機械手動力學問題；RakhshaandGoldenberg利用Newton—Euler法和假定模態法研究了單桿柔性機械手動力學問題；AkiraAbe和Andr6Fenili利用Lagrange方程和假定模態法建立了兩桿剛柔機械手的動力學模型。但是對於多桿構件，構件的模態相互作用所導致的模態共振現象，該方法並沒有考慮；對於複雜截面、複雜載荷的多構件柔性機械手動力學分析，該方法也不適用。
有限元法也是建立在Lagrange或Newton—Euler原理基礎上。它是把無限個自由度的連續體理想化為有限個自由度的單元集合體，使問題簡化為適合數值解法的結構型問題。其特點是採用彈性單元、剛性結點、載荷向結點移置、剛度及阻尼特性由單元表征。有限元法非常適合複雜形狀、邊界和載荷情況下的物體作離散和分析，其邊界條件和幾何物理特性可以直接描述。BianYushu¨叫和MohamedandTokhi採用有限元法研究柔性機械手；MoulinandBayoc利用有限元法研究了柔性機械手逆動力學問題，在頻域內求得了關節驅動力，在該驅動力作用下，機械手可以準確地跟蹤給定軌跡；Tokhi套用有限元法建立了單桿柔性機械手動力模型，並將結果與實驗所得模態所構建的動力學模型進行比較，驗證了模型的正確性；RosadoandYuhara和Rosado套用Newton—Euler方程和有限元法，綜合考慮了構件和關節的彈性變形，構建了兩桿平面機械手動力學模型。該方法所得動力學方程較為複雜，動態回響求解運算量也較大。但是由於沒有考慮構件大範圍運動與彈性變形問動力學耦合問題，該方法套用範圍有限，僅適用於低速、小變形情況。
集中質量法是將整個機械手看做是彈簧和質量塊的綜合，用若干離散結點上的集中質量代替原來系統中的分布質量，整個動力方程都能直接通過對質量的近似離散化處理得到。MegahedandHamza，Raboud等學者在這方面進行了很多的研究工作。該方法是最簡便的分析方法，但求解精確度不高。
動力學模型建立方法
柔性機械手的彈性變形導致振動現象出現。很多研究者通過提高動力學模型的精確度和採用不同的控制策略來解決。無論是連續或離散的柔性機械手動力學模型，其建模方法主要基於矢量力學和分析力學。Newton—Euler公式、Lagrange方程、變分原理、Kane方程和虛功原理是套用較廣泛同時也是比較成熟的。
(1)Newton—Euler公式。
Newton—Euler法又稱為D’Alembert原理，主要考慮慣性力與主動力和約束力的平衡，對於柔性桿要考慮彈性力。Newton—Euler公式套用質心動量矩定理寫出隔離體的動力學方程，在動力學方程中出現相鄰體間的內力項，其物理意義明確表達了系統完整的受力關係，並且具有良好的開放性。
(2)Lagrange方程。
Lagrange方程是用系統的動能對廣義坐標和廣義速度的偏導數表示的動力學方程。Hamilton正則方程與Lagrange方程完全等價。套用Lagrange方程時，求出能量函式，以能量方式建模，可以避免方程中出現內力項。Lagrange方程在完整系統中套用廣泛且方便，對於非完整系統可採用Lagrange乘子。AndrFenili利用Lagrange方程建立了兩桿剛柔機械手的動力學模型；Martins，Tso和楊玉維利用Lagrange方程對單桿柔性機械手進行了研究；該方法在使用時需要對時間求導，使求解過程變得繁瑣，尤其對於柔性系統，由於系統構型隨著時間變化，微分運算過程更加複雜。
(3)變分原理。
Gauss原理和Hamihon原理是兩種套用最普遍的變分原理。變分原理不需要建立動力學微分方程，可直接套用最佳化計算方法進行動力學分析。變分原理將真實發生的運動與約束允許的可能運動加以比較，將系統真實運動應滿足的條件表示為某個函式或泛函的極值條件，並利用此條件確定系統的運動，從而提供了一種能將真實運動從可能運動中甄別出來的準則。這種方法可結合控制系統的最佳化進行綜合分析，便於動力學分析向控制模型的轉化。BarunPratihe套用擴展的Hamilton原則建立柔性單桿動力學模型；Efiy.chiosG，Christoforou利用Lagrange公式和Hamilton原理對柔性機械臂進行了深入的研究工作；HassanZo—hoor利用Hamilton原理獲得柔性兩桿飛行機械手的柔性動力學方程。這種方法開闢了一個不必建立運動微分方程的新途徑，可直接運用最佳化計算方法進行動力學分析。
(4)Kane方程。
Kane方法是建立多體系統動力學方程的又一種方法，它是基於D’Alembert原理，利用廣義速率代替廣義坐標作為獨立變數來描述系統的運動，從而導出動力學方程，Kane將這種方法稱為Lagrange形式的D’Alembert原理。負今天、王樹新、丁傑利用Kane方程建立了任意形狀柔性體動力學方程和一般柔性多體系統的動力學方程[胡權，賈英宏，徐世傑對Kane方程進行擴展，建立了不含待定乘子適用於任意多體系統的動力學模型。該方法可消除方程中的內力項，避免使用動力學函式求導的繁瑣運算，使推導過程較為系統化，適用於計算機符號推導和編程，但是它不直觀。
(5)虛功原理。
把虛位移原理與D’Alembert原理結合起來，就成為可以解決具有理想約束系統的動力學問題的虛功原理。虛功原理與Kane方法類似。薛克宗、趙平口利用虛功原理建立了柔性多體系統的微分方程。該方法建立的方程中不含約束反力，不能直接求出約束反力。
機械手構成
編輯
機械手主要由執行機構、驅動機構和控制系統三大部分組成。手部是用來抓持工件（或工具）的部件，根據被抓持物件的形狀、尺寸、重量、材料和作業要求而有多種結構形式，如夾持型、托持型和吸附型等。運動機構，使手部完成各種轉動（擺動）、移動或複合運動來實現規定的動作，改變被抓持物件的位置和姿勢。運動機構的升降、伸縮、旋轉等獨立運動方式，稱為機械手的自由度。為了抓取空間中任意位置和方位的物體，需有6個自由度。自由度是機械手設計的關鍵參數。自由度越多，機械手的靈活性越大，通用性越廣，其結構也越複雜。一般專用機械手有2～3個自由度。控制系統是通過對機械手每個自由度的電機的控制，來完成特定動作。同時接收感測器反饋的信息，形成穩定的閉環控制。控制系統的核心通常是由單片機或dsp等微控制晶片構成，通過對其編程實現所要功能。
執行機構
機械手的執行機構分為手部、手臂、軀幹；
1、手部
手部安裝在手臂的前端。手臂的內孔中裝有傳動軸，可把運用傳給手腕，以轉動、伸曲手腕、開閉手指。
機械手手部的構造系模仿人的手指，分為無關節、固定關節和自由關節3種。手指的數量又可分為二指、三指、四指等，其中以二指用的最多。可根據夾持對象的形狀和大小配備多種形狀和大小的夾頭以適應操作的需要。所謂沒有手指的手部，一般都是指真空吸盤或磁性吸盤。
2、手臂
手臂的作用是引導手指準確地抓住工件，並運送到所需的位置上。為了使機械手能夠正確地工作，手臂的3個自由度都要精確地定位。
3、軀幹軀幹是安裝手臂、動力源和各種執行機構的支架。
驅動機構
機械手所用的驅動機構主要有4種：液壓驅動、氣壓驅動、電氣驅動和機械驅動。其中以液壓驅動、氣壓驅動用得最多。
1、液壓驅動式
液壓驅動式機械手通常由液動機（各種油缸、油馬達）、伺服閥、油泵、油箱等組成驅動系統，由驅動機械手執行機構進行工作。通常它的具有很大的抓舉能力（高達幾百千克以上），其特點是結構緊湊、動作平穩、耐衝擊、耐震動、防爆性好，但液壓元件要求有較高的製造精度和密封性能，否則漏油將污染環境。
2、氣壓驅動式
其驅動系統通常由氣缸、氣閥、氣罐和空壓機組成，其特點是氣源方便、動作迅速、結構簡單、造價較低、維修方便。但難以進行速度控制，氣壓不可太高，故抓舉能力較低。
3、電氣驅動式電力驅動是機械手使用得最多的一種驅動方式。其特點是電源方便，回響快，驅動力較大（關節型的持重已達400kg），信號檢測、傳動、處理方便，並可採用多種靈活的控制方案。驅動電機一般採用步進電機，直流伺服電機（AC）為主要的驅動方式。由於電機速度高，通常須採用減速機構（如諧波傳動、RV擺線針輪傳動、齒輪傳動、螺旋傳動和多桿機構等）。有些機械手已開始採用無減速機構的大轉矩、低轉速電機進行直接驅動（DD）這既可使機構簡化，又可提高控制精度。
4、機械驅動式
機械驅動只用於動作固定的場合。一般用凸輪連桿機構來實現規定的動作。其特點是動作確實可靠，工作速度高，成本低，但不易於調整。其他還有採用混合驅動，即液-氣或電-液混合驅動。
控制系統
機械手控制的要素包括工作順序、到達位置、動作時間、運動速度、加減速度等。機械手的控制分為點位控制和連續軌跡控制兩種。
控制系統可根據動作的要求，設計採用數字順序控制。它首先要編製程序加以存儲，然後再根據規定的程式，控制機械手進行工作程式的存儲方式有分離存儲和集中存儲兩種。分離存儲是將各種控制因素的信息分別存儲於兩種以上的存儲裝置中，如順序信息存儲於插銷板、凸輪轉鼓、穿孔帶內；位置信息存儲於時間繼電器、定速迴轉鼓等；集中存儲是將各種控制因素的信息全部存儲於一種存儲裝置內，如磁帶、磁鼓等。這種方式使用於順序、位置、時間、速度等必須同時控制的場合，即連續控制的情況下使用。
其中插銷板使用於需要迅速改變程式的場合。換一種程式只需抽換一種插銷板限可，而同一外掛程式又可以反覆使用；穿孔帶容納的程式長度可不受限制，但如果發生錯誤時就要全部更換；穿孔卡的信息容量有限，但便於更換、保存，可重複使用；磁蕊和磁鼓僅適用於存儲容量較大的場合。至於選擇哪一種控制元件，則根據動作的複雜程式和精確程式來確定。對動作複雜的機械手，採用求教再現型控制系統。更複雜的機械手採用數字控制系統、小型計算機或微處理機控制的系統。控制系統以插銷板用的最多，其次是凸輪轉鼓。它裝有許多凸輪，每一個凸輪分配給一個運動軸，轉鼓運動一周便完成一個循環。
