定義
簡單隨機樣本
定義1 設X,X,...,X是來自總體X的容量為n的樣本,如果X,X,...,X相互獨立且每一個都是與總體X有相同分布的隨機變數,則稱X,X,...,X為總體X的容量為n的 簡單隨機樣本,簡稱為簡單樣本或樣本。
註:樣本X,X,...,X也可用n維隨機向量 (X,X,...,X) 表示。記x為X的一次觀察值,並稱(x,x,...,x)為樣本X,X,...,X的一次觀察值。
樣本統計量
定義2 設X,X,...,X為總體X的樣本,T為n維實值函式,作樣本X,X,...,X的函式T=T(X,X,...,X)(不帶未知參數的隨機變數),T的取值記為t=T(x,x,...,x),稱T或T(X,X,...,X)為 樣本統計量,簡稱為 統計量。
註:1)統計量指的是樣本的函式,並且不含有未知參數。樣本的函式等價於定義在樣本空間上的函式。
2)給定樣本的一次觀察值x=(x,x,...,x) 時,T(x,x,...,x)的值完全確定。
舉例
例1 設X,X,...,X為總體X的樣本,其容量為n. 記
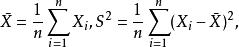 樣本統計量
樣本統計量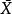 樣本統計量
樣本統計量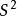 樣本統計量
樣本統計量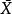 樣本統計量
樣本統計量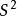 樣本統計量
樣本統計量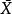 樣本統計量
樣本統計量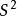 樣本統計量
樣本統計量則及都是統計量,稱及分別為樣本X,X,...,Xn的平均值及方差。樣本的觀察值為x,x,...,x及的觀察值分別記作
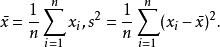 樣本統計量
樣本統計量拓展
順序統計量
定義3 設X,X,...,X為總體X的樣本,今由樣本建立n個函式:
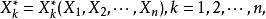 樣本統計量
樣本統計量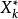 樣本統計量
樣本統計量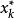 樣本統計量
樣本統計量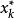 樣本統計量
樣本統計量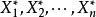 樣本統計量
樣本統計量其中為這樣的 統計量,它的觀察值為,為樣本X,X,...,X的觀察值x,x,...,x中由小到大排列後的第k為數值,則稱為 順序統計量。
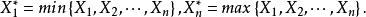 樣本統計量
樣本統計量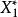 樣本統計量
樣本統計量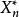 樣本統計量
樣本統計量註:易見, 稱為最小項統計量,為最大項統計量。
極差
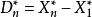 樣本統計量
樣本統計量定義4 設X,X,...,X為總體X的樣本,則稱統計量為樣本的 極差。
註:極差是樣本中最大值與最小值之差,反映了樣本觀察值的波動幅度。它同方差一樣是反映觀察值離散程度的數量指標,而且計算方便。
抽樣分布
統計量是對總體X的分布函式或數字特徵進行估計與推斷最重要的基本概念,求出統計量T(x,x,...,x)的分布函式是數理統計學的基本問題之一。統計量的分布,稱為 抽樣分布。
