模擬信號的數字傳輸簡介
1 模擬信號數字傳輸的優點
當數位訊號經過多次轉換、中繼、遠距離傳輸後信噪比的程度會降低，而模擬信號經過多次中繼後會產生比較嚴重的信噪比惡化，嚴重降低傳輸信號的質量。
模擬信號數位化以後可以很方便地進行時分或碼分多路傳輸，從而可有效地提高信道的利用率。
模擬信號的數字傳輸技術已廣泛套用於現代通信的各個領域，從有線的程控交換機到無線的GSM、CDMA手機，從衛星數位電視廣播到長途光纖通信到處都有數位化的信號存在。
2 模擬信號數字傳輸系統的組成框圖
通信系統可以分為模擬通信系統和數字通信系統，其傳輸信號的方式如下圖1所示。
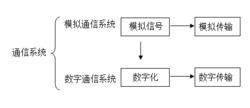圖1 通信系統傳輸方式示意圖模擬信號數位化後，用數字通信方式傳輸。
傳送端先將模擬訊息的信號抽樣，使其成為一離散的抽樣值；然後將抽樣值量化為相應的量化值；
經編碼變換成數位訊號，用數字通信方式傳輸；在接收端則相應地將接收到的數位訊號恢復成模擬訊息。
模擬信號的數字傳輸的框圖如圖2所示。
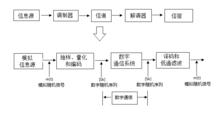圖2 模擬信號數字傳輸的框圖3 模擬信號數位化的基本原理
模擬信號數位化過程中的處理如圖3所示。
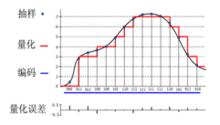圖3 模擬信號數位化的基本原理模擬信號的抽樣
抽樣定理
抽樣定理指出：設一個連續模擬信號m(t)中的最高頻率小於fH，則以間隔時間為T（小於等於1/(2fH)）的周期性衝激脈衝對它抽樣時，m(t)將被這些抽樣值所完全確定。由於抽樣時間間隔相等，所以此定理又稱為均勻抽樣定理。
模擬信號通常是在時間上連續的信號。在一系列離散點上，對這種信號抽取樣值稱為抽樣。在理論上，抽樣過程可以看作是用周期性單位衝激脈衝和此模擬信號相乘，如圖4所示。
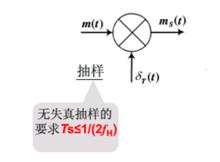圖4 模擬信號的抽樣過程在實際上，是用周期性窄脈衝代替衝激脈衝與模擬信號相乘，可以證明，這樣抽樣時，抽樣定理仍然正確。從另一個角度看，可以把周期性脈衝序列看作是非正弦載波，而抽樣過程可以看作是用模擬信號對它進行振幅調製。這種調製稱為脈衝振幅調製（PAM）。可以將PAM信號的振幅變化按比例地變換成脈衝寬度的變化，得到脈衝寬度調製（PDM）。或者，變換成脈衝相位（位置）的變化，得到脈衝位置調製（PPM）。這些種類的調製，雖然在時間上都是離散的，但是仍然是模擬調製，因為其代表信息的參量仍然是可以連續變化的。這些已調信號當然也屬於模擬信號。
抽樣所得離散衝激脈衝顯然和原始連續模擬信號形狀不一樣。根據抽樣定理，不一定要傳輸模擬信號本身，可以只傳輸這些離散的抽樣值，接收端就能恢復原始的模擬信號，如圖5所示。
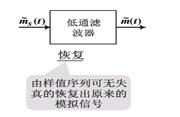圖5 接收端對模擬信號的恢復抽樣定理為模擬信號的數位化奠定了理論基礎。
實際中遇到的許多信號是帶通型信號。如果採用低通抽樣定理的抽樣速率fs（fs大於等於2fH），對頻率限制在fL和fH之間的帶通型信號抽樣，肯定能滿足頻譜不混疊的要求。但這樣選擇fs太高了，它會使0~fL頻譜空隙得不到利用，抽樣後的信號速率很高，降低了信道的利用率。可以證明，此帶通型模擬信號所需最小抽樣速率fs等於
fs=2B(1+(k/n))
式中：B為信號頻寬，B=fH-fL；n為fH/B的整數部分；k為fH/B的小數部分。
模擬信號的量化
抽樣後的離散模擬信號，必須經過量化才成為數位訊號，如圖6所示。
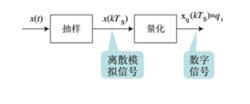圖6 抽樣後的離散模擬信號的量化為數位訊號抽樣過程是時間上的離散化，量化問題是幅度上取離散值。從數學上看，量化過程是把一連續幅度的無限集合映射成一個離散幅度的有限集合。
量化過程包括分層和量化。若我們僅用N個二進制數字碼元代表此抽樣值的大小，則N個二進制碼元最多只能代表M=2的N次方個不同的抽樣值。因此，必須將抽樣值的範圍劃分成M個區間，每個區間用一個電平表示。這樣，共有M個離散電平，它們稱為量化電平。用這M個量化電平表示連續抽樣值的方法稱為量化。
量化問題可以分為標量量化和矢量量化。其中，標量量化又可分為均勻量化和非均勻量化。
均勻量化
設模擬抽樣信號的取值範圍在a和b之間，量化電平數為M，則在均勻量化時量化間隔為
Δv=（b-a）/M
量化輸出電平可以取量化區間的端點，也可以取量化區間的中點。量化過程如圖7所示。
圖7 量化過程示意圖顯然，量化輸出電平和量化前信號的抽樣值一般不同，即量化輸出電平有誤差。這個誤差稱為量化噪聲，並用信號功率與量化噪聲之比（簡稱信號量噪比）衡量此誤差對於信號影響的大小。對於給定的信號最大幅度，量化電平數越多，量化噪聲越小，信號量噪比越高。
非均勻量化
在非均勻量化時，量化間隔是隨信號抽樣值的不同而變化的。信號抽樣值小時，量化間隔Δv也小；信號抽樣值大時，量化間隔Δv也變大。實際中，非均勻量化的實現方法通常是在進行量化之前，先將信號抽樣值壓縮，再進行均勻量化。這裡的壓縮是用一個非線性電路將輸入電壓變換成輸出電壓。
編碼
量化後的信號，已經是取值離散的數位訊號。下一步的問題是如何將這個數位訊號編碼。最最常用的編碼是用二進制的符號表示離散數值。通常把從模擬信號抽樣、量化，直到變換成為二進制符號的基本過程，稱為脈衝編碼調製（PCM），簡稱脈碼調製。不同編碼方法比較如圖8所示。
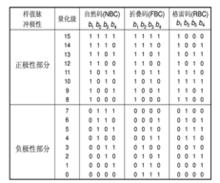圖8 三種不同編碼方法的比較編碼極性
上述圖中：
0~7的8個量級對應負極性樣值脈衝；8~15的8個量級對應正極性樣值脈衝。
碼元b1表示極性，b1=1表示正極性，b1=0表示負極性。其餘三位表示信號的絕對值。
自然碼（NBC）
此類二進制編碼，是按照二進制數的自然規律排列的，稱為自然二進制碼。例如：第11個量化級，11=2^3+0+2^1+2^0，對應碼組1011。另外，除碼元b1以外，上下兩部分是相同的。
摺疊碼（FBC）
除碼元b1以外，上下兩部分呈摺疊關係。絕對值相同，則編碼相同，也即表現單極性編碼，簡化編碼過程。出現誤碼時，對小信號影響小，對大信號影響大。例如：1000到0000，僅差一個量化級，而自然碼差8個量化級。話音信號小幅度出現的機率比大幅度的大，平均誤差功率減小。PCM標準中採用摺疊碼。
格雷碼（RBC）
任何相鄰電平的碼組，只有一位碼位發生變化，即相鄰碼字的距離恆為1。解碼時，若傳輸或判決有誤，造成的誤差小。不能逐比特獨立進行編碼和解碼，需先轉換為自然二進制碼後再解碼，編解碼電路複雜。
