定義
對於時間函式 f( t), 其線性時頻變換可以定義為
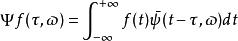 標準時頻變換
標準時頻變換 其中:
 標準時頻變換
標準時頻變換 表示當地時間,也可被認為考察時刻;
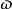 標準時頻變換
標準時頻變換 表示當地頻率,也可被認為考察頻率;
上劃線表示共軛運算元;
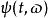 標準時頻變換
標準時頻變換 稱為核函式。
 標準時頻變換
標準時頻變換 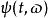 標準時頻變換
標準時頻變換 一個線性時頻變換被稱為一個標準時頻變換,如果其核函式的傅立葉變換
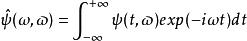 標準時頻變換
標準時頻變換 滿足
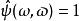 標準時頻變換
標準時頻變換  標準時頻變換
標準時頻變換 i)當;
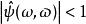 標準時頻變換
標準時頻變換 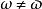 標準時頻變換
標準時頻變換 ii) ,當。
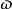 標準時頻變換
標準時頻變換 解釋:首先,標準時頻變換是以為索引下的卷積,這是它的本質之一。在這一點上它與小波變換類似,但它與短時傅立葉變換及S變換有著本質的區別。其次,標準時頻變換有著如條件i)和ii)所示的標準化含義,這種含義將在如下的描述中體現出意義。
無為原理
對於一個和諧信號
 標準時頻變換
標準時頻變換 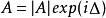 標準時頻變換
標準時頻變換  標準時頻變換
標準時頻變換  標準時頻變換
標準時頻變換 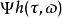 標準時頻變換
標準時頻變換 其中是複數振幅、是角頻率、是初相位,其標準時頻變換滿足如下關係
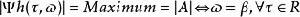 標準時頻變換
標準時頻變換 1)
 標準時頻變換
標準時頻變換 2)
 標準時頻變換
標準時頻變換 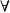 標準時頻變換
標準時頻變換 其中表示“若且唯若”,表示“對於任意”, R 表示實數域。
 標準時頻變換
標準時頻變換 上述就是所謂的無為原理,它可簡述為:一個和諧信號的標準時頻變換沿譜脊線的取值正是這個和諧信號本身。關係1)表明,一個和諧信號的標準時頻譜(振幅譜)極大值可以確定出這個和諧信號的頻率和振幅| A|,而關係 2)則表明沿著譜極大值線(脊線),和諧信號自動就顯現出來(包含了當地相位)。這裡,和諧信號的顯現既沒有利用逆變換,也沒有利用濾波手段。如果非要說濾波,無為原理揭示的也是一種“線通”濾波思想。
無為原理於2007被柳林濤發現 ,它是提出標準時頻變換這一概念的基礎。無為原理於2016年被俄羅斯科學家利用小波變換再次宣布 。
利用無為原理,人們可以提取時間序列中的周期項,更廣義地講,可以利用無為原理提取序列中的準周期項(如Chirp信號)。這種利用無為原理提取時間序列中周期及準周期項的方法稱為無為方法。無為方法具體操作如下:對時間序列做標準時頻變換,再得到時頻譜,找到譜脊線,沿著譜脊線的標準時頻變換值就是對周期信號的提取或對準周期信號的逼近。
2016年,王國成發現了無為方法的魯棒性 。也就是說,無為方法這種線通濾波手段有很好的抗噪聲能力,這是NTFT理論上的進展。
逆變換
行文至此,人們還不知道標準時頻變換的核函式的具體表達式,但可以給出NTFT的逆變換如下
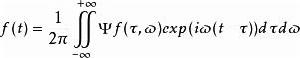 標準時頻變換
標準時頻變換 這個公式於2009年給出,它是反卷積定理 的一個簡單推論。該逆變換公式與上述的無為原理共同構成標準時頻變換的理論基礎。該逆變換可用於時頻濾波。不過由於實際數據往往含有噪聲,時頻濾波很難隔離噪聲的影響,這限制了逆變換的實際套用。
核函式
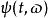 標準時頻變換
標準時頻變換 標準時頻變換的核函式可具體表達為多種形式,這裡嘗試給出如下形式,
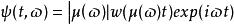 標準時頻變換
標準時頻變換 其中
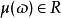 標準時頻變換
標準時頻變換 是無量綱的尺度調整函式;
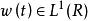 標準時頻變換
標準時頻變換 是一個標準窗。
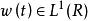 標準時頻變換
標準時頻變換 標準窗的定義為:被稱為一個標準窗,如果其傅立葉變換滿足:
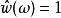 標準時頻變換
標準時頻變換  標準時頻變換
標準時頻變換 i),當;
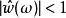 標準時頻變換
標準時頻變換 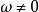 標準時頻變換
標準時頻變換 ii),當。
一個經典的標準窗是標準高斯窗,如下 ,
 標準時頻變換
標準時頻變換 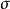 標準時頻變換
標準時頻變換 其中為正的常數,它與 t同量綱。
 標準時頻變換
標準時頻變換 至此,人們可以檢驗一下: f( t)與它的標準時頻變換是同量綱的,這是無為原理能夠成立的一種原因。
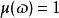 標準時頻變換
標準時頻變換 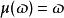 標準時頻變換
標準時頻變換 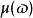 標準時頻變換
標準時頻變換 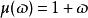 標準時頻變換
標準時頻變換 無量綱的尺度調整函式可以有無限種設定形式。當設定,標準時頻變換就是一種標準加伯變換(或標準短時傅立葉變換),這時,傳統加伯變換已經由非卷積形式變為卷積形式了。當設定,標準時頻變換就是一種標準小波變換,只是這種小波變換是L1-norm形式,而非傳統的L2-norm形式。當設定成其他形式,如,這時的標準時頻變換就是一種未被探索的新變換了。
在具體的套用中,一般可採用標準加伯變換或標準小波變換。
時頻譜
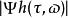 標準時頻變換
標準時頻變換 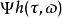 標準時頻變換
標準時頻變換 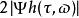 標準時頻變換
標準時頻變換 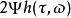 標準時頻變換
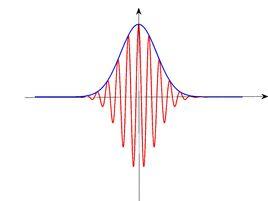
標準時頻變換 標準時頻變換提供兩種譜:振幅譜和相位譜。由振幅譜可以觀察信號振幅及頻率隨著時間的變化,由相位譜可以看出信號相位隨著時間的分布。如果 f( t)是複數,則就是其振幅譜,而的實部與虛部共同組成其相位譜。如果 f( t)是實數(見圖1),則就是其振幅譜(見圖2),而的實部即其相位譜(見圖3)。
 實例時頻圖
實例時頻圖 預測模型
 標準時頻變換
標準時頻變換  標準時頻變換
標準時頻變換  標準時頻變換
標準時頻變換 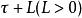 標準時頻變換
標準時頻變換 對於如上的和諧信號 h( t),如果我們通過無為方法確定了其在時刻的值及其頻率,那么,該和諧信號在未來時刻的值可以如下預測:
 標準時頻變換
標準時頻變換 這就是標準時頻變換用來預測的基本模型。
邊緣效應
標準時頻變換普遍存在邊緣效應。這一效應是指變換在數據的頭尾附近產生畸變。產生邊緣效應的本質原因在數據頭尾以外的數據未知。如何有效地減緩邊緣效應是時頻分析領域的重要課題,尤其對於預測學十分重要。相關研究正在進行。
套用與展望
標準時頻變換已經在地球科學中得到成功套用。例如,1)地球極移的分析與預測 ;2)地球日長六年信號振幅衰減現象的發現 ;3)地球自由振盪的檢測 ;4)潮汐預測 ;5)衛星鐘差周期信號的提取等等。
除了上述套用,相信標準時頻變換還可以在雷達、聲吶、通訊、醫學信號分析與處理中得到套用,相關研究正處於開始階段。