定義
標準常態分配---standard normal distribution
常態分配標準常態分配又稱為u分布，是以0為均數、以1為標準差的常態分配，記為N（0，1）。
標準常態分配曲線下面積分布規律是：在-1.96～+1.96範圍內曲線下的面積等於0.9500，在-2.58～+2.58範圍內曲線下面積為0.9900。統計學家還制定了一張統計用表（自由度為∞時），藉助該表就可以估計出某些特殊u1和u2值範圍內的曲線下面積。
附表 標準常態分配表
標準常態分配（點擊可放大）
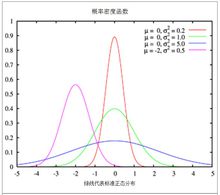標準常態分配常態分配的機率密度函式曲線呈鐘形，因此人們又經常稱之為鐘形曲線。我們通常所說的標準常態分配是位置參數均數為0, 尺度參數：標準差為1的常態分配（見右圖中綠色曲線）。
常態分配中一些值得注意的量：
密度函式關於平均值對稱
平均值與它的眾數（statistical mode）以及中位數（median）同一數值。
函式曲線下68.268949%的面積在平均數左右的一個標準差範圍內。
95.449974%的面積在平均數左右兩個標準差的範圍內。
99.730020%的面積在平均數左右三個標準差的範圍內。
99.993666%的面積在平均數左右四個標準差的範圍內。
函式曲線的反曲點（inflection point）為離平均數一個標準差距離的位置。
標準偏差
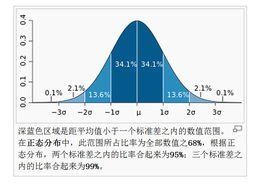標準常態分配深藍色區域是距平均值小於一個標準差之內的數值範圍。在常態分配中，此範圍所占比率為全部數值之68%，根據常態分配，兩個標準差之內的比率合起來為95%；三個標準差之內的比率合起來為99%。
在實際套用上，常考慮一組數據具有近似於常態分配的機率分布。若其假設正確，則約68.3%數值分布在距離平均值有1個標準差之內的範圍，約95.4%數值分布在距離平均值有2個標準差之內的範圍，以及約99.7%數值分布在距離平均值有3個標準差之內的範圍。稱為“68-95-99.7法則”或“經驗法則”。
