梯度消失問題
下圖是神經網路在訓練過程中, 隨epoch增加時各種隱藏層的學習率變化。
兩個隱藏層：[784,30,30,10]
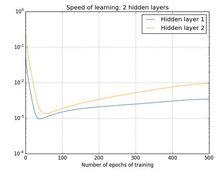兩個隱藏層三個隱藏層：[784,30,30,30,10]
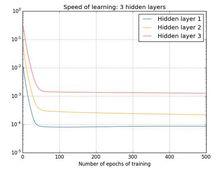三個隱藏層四個隱藏層：[784,30,30,30,30,10]
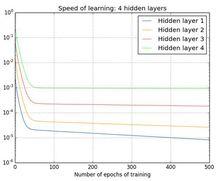四個隱藏層可以看到：前面的隱藏層的學習速度要低於後面的隱藏層。這種現象普遍存在於神經網路之中， 叫做消失的梯度問題（vanishing gradient problem）。更加一般地說，在深度神經網路中的梯度是不穩定的，在前面的層中或會消失，或會激增。這種不穩定性才是深度神經網路中基於梯度學習的根本問題 。
產生梯度消失問題的原因
下圖是一個極簡單的深度神經網路：每一層都只有一個單一的神經元。
深度神經網路代價函式C對偏置b的偏導數的結果計算如下：
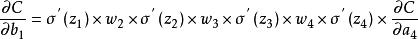梯度消失問題sigmoid 函式導數的圖像如圖：
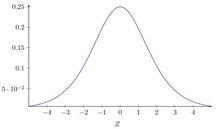sigmoid函式導數該導數在σ′(0) = 1/4時達到最高。現在，如果我們使用標準方法來初始化網路中的權重，那么會使用一個均值為0 標準差為1 的高斯分布。因此所有的權重通常會滿足|w|<1。從而有wσ′(z) < 1/4。這就是消失的梯度出現的本質原因。
根本的問題其實並非是消失的梯度問題或者激增的梯度問題，而是在前面的層上的梯度是來自後面的層上項的乘積。所以神經網路非常不穩定。唯一可能的情況是以上的連續乘積剛好平衡大約等於1，但是這種幾率非常小 。
解決方案
預訓練加微調
Hinton為了解決梯度的問題，提出採取無監督逐層訓練方法，其基本思想是每次訓練一層隱節點，訓練時將上一層隱節點的輸出作為輸入，而本層隱節點的輸出作為下一層隱節點的輸入，此過程就是逐層“預訓練”（pre-training）；在預訓練完成後，再對整個網路進行“微調”（fine-tunning）。Hinton在訓練深度信念網路（Deep Belief Networks中，使用了這個方法，在各層預訓練完成後，再利用BP算法對整個網路進行訓練。此思想相當於是先尋找局部最優，然後整合起來尋找全局最優。
梯度剪下、正則
梯度剪下這個方案主要是針對梯度爆炸提出的，其思想是設定一個梯度剪下閾值，然後更新梯度的時候，如果梯度超過這個閾值，那么就將其強制限制在這個範圍之內。
另外一種解決梯度爆炸的手段是採用權重正則化（weithts regularization）比較常見的是l1正則，和l2正則，在各個深度框架中都有相應的API可以使用正則化，比如在tensorflow中，若搭建網路的時候已經設定了正則化參數，則調用以下代碼可以直接計算出正則損失：
regularization_loss = tf.add_n(tf.losses.get_regularization_losses(scope="my_resnet_50"))
如果沒有設定初始化參數，也可以使用以下代碼計算l2正則損失：
l2_loss = tf.add_n([tf.nn.l2_loss(var) for var in tf.trainable_variables() if 'weights' in var.name])
relu、leakrelu、elu等激活函式
Relu :如果激活函式的導數為1，那么就不存在梯度消失的問題了，每層的網路都可以得到相同的更新速度，relu就這樣應運而生。先看一下relu的數學表達式：
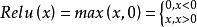梯度消失問題其函式圖像為：
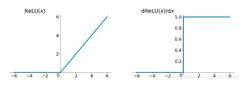ReLU函式可以看出，relu函式的導數在正數部分是恆等於1的，因此在深層網路中使用relu激活函式就不會導致梯度消失的問題。
relu的主要貢獻在於：1. 解決了梯度消失、爆炸的問題 -- 計算方便，計算速度快 。2. 加速了網路的訓練
同時也存在一些缺點：1. 由於負數部分恆為0，會導致一些神經元無法激活（可通過設定國小習率部分解決） 2. 輸出不是以0為中心的。
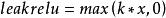梯度消失問題leakrelu解決了relu的0區間帶來的影響，其數學表達為：其中k是leak係數，一般選擇0.01或者0.02，或者通過學習而來 。
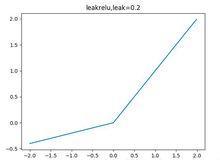leakreluelu激活函式也是為了解決relu的0區間帶來的影響，其數學表達為：
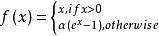梯度消失問題其函式及其導數數學形式為：
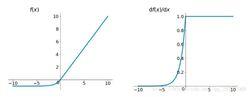elu函式LSTM
LSTM全稱是長短期記憶網路（long-short term memory networks），是不那么容易發生梯度消失的，主要原因在於LSTM內部複雜的“門”(gates)，如下圖，LSTM通過它內部的“門”可以接下來更新的時候“記住”前幾次訓練的”殘留記憶“，因此，經常用於生成文本中 。
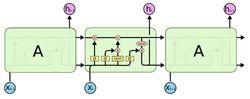LSTM