定律定義
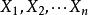 格里文科定理
格里文科定理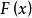 格里文科定理
格里文科定理 格里文科定理
格里文科定理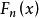 格里文科定理
格里文科定理設 是來自以 為分布函式的總體 的樣本, 是經驗分布函式,則有
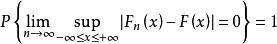 格里文科定理
格里文科定理推導過程
 格里文科定理
格里文科定理 格里文科定理
格里文科定理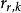 格里文科定理
格里文科定理 格里文科定理
格里文科定理將 的取值離散化,對任意正整數 ,記 表示滿足下述不等式的最大 :
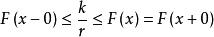 格里文科定理
格里文科定理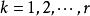 格里文科定理
格里文科定理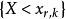 格里文科定理
格里文科定理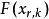 格里文科定理
格里文科定理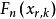 格里文科定理
格里文科定理則事件 發生的機率為 ,其出現的頻率為 ,由大數定律()知
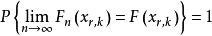 格里文科定理
格里文科定理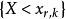 格里文科定理
格里文科定理類似地,考察事件 ,有
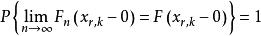 格里文科定理
格里文科定理定義事件
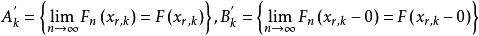 格里文科定理
格里文科定理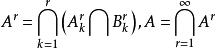 格里文科定理
格里文科定理於是
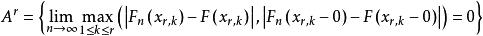 格里文科定理
格里文科定理注意到
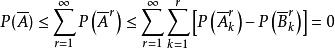 格里文科定理
格里文科定理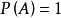 格里文科定理
格里文科定理即 ,記
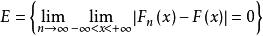 格里文科定理
格里文科定理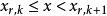 格里文科定理
格里文科定理 格里文科定理
格里文科定理現對任何滿足 的 ,有
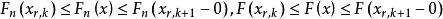 格里文科定理
格里文科定理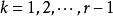 格里文科定理
格里文科定理由此可得,當 時:
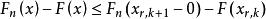 格里文科定理
格里文科定理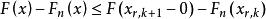 格里文科定理
格里文科定理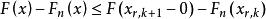 格里文科定理
格里文科定理同理
 格里文科定理
格里文科定理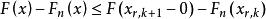 格里文科定理
格里文科定理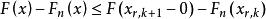 格里文科定理
格里文科定理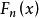 格里文科定理
格里文科定理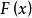 格里文科定理
格里文科定理於是,我們證明了 包含於 ,因此
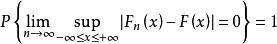 格里文科定理
格里文科定理實驗驗證
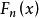 格里文科定理
格里文科定理定律影響
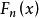 格里文科定理
格里文科定理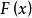 格里文科定理
格里文科定理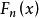 格里文科定理
格里文科定理定理的含義是 在整個實軸上以機率1均勻收斂於 .於是當樣本容量 充分大時, 能良好地逼近總體分布函式.這是在統計學中以樣本推斷總體的依據.
